Difference between revisions of "Team:Valencia UPV/Model"

Latest revision as of 02:22, 18 October 2018

Stack Multipurpose HTML Template

Index

Models & Experiments
Simulation Tool
References

Do you think it is possible to mathematically describe a cell? Would you like to know the possibilities that modeling offers you?

One of the fundamental bases of Printeria has undoubtedly been mathematical modeling. Thanks to the development and application of new mathematical models, it is possible to quantify the expression of proteins in cells, and therefore characterize through different experiments the parts designed by Printeria. From the Printeria Modeling team, we intend to reach different goals:

Design simple mathematical models based on differential equations that describe the biochemical processes of a cell. With them, we can simulate the different genetic circuits that Printeria allows us to build.
Develop a Simulation Tool that allows the user to visualize a prediction of the results of their experiment before running it in Printeria.
Optimize model parameters to match simulation results to experimental data obtained from Printeria constructions.
Characterize the parts of our Part Collection from the optimization results and provide the user with all the information about the Printeria kit.

Although in the development of the project we have dealt with all these aspects, all of them have a single purpose: demonstrate the importance and many applications of describing in a mathematical way the biological processes that take place inside the cell.

Models & Experiments

The development of new and simple mathematical models has been one of the essential bases of the Printeria project. The ODE models offer a multitude of applications: describing the basic biochemical reactions of the cell, to characterizing the parts of our Printeria kit by means of different experiments, and elaborating new tools that facilitate the user learn about Synthetic Biology.

In Printeria Modeling team, we have grouped the models designed in two fields: constitutive expression models and inducible expression models. We have also established an experimental protocol and a multi-objective optimization protocol in order to contrast theoretical and experimental results. With them, we can describe practically all the cells modified with Printeria.

Want to find out more about how we did it?

Modeling process

At the beginning of the design of any mathematical model, we have started from a cell scheme in which all the biochemical reactions happen. From the reactions, a set of equations is inferred. Each of these equations describe the temporal evolution of the main biochemical species in the cell (DNA, RNA, proteins and transcription factors), and depend on a set of parameters with a physical meaning.

Modeling process schema.

Because they are ordinary differential and generally non-linear equations (ODE), mathematical models are simulated using software tools such as MATLAB. The results obtained from the simulation reflect the evolution of the concentration of biochemical species over time. These theoretical results can be contrasted with the experimental data obtained in the laboratory and thereby adjust the parameters. The ODE model fits the data in an optimal way. This process, called multiobjective parameter optimization, is the process that allows us to validate our models and see if they respond to what happens inside the cells.

The development of the set of mathematical models of the genetic circuits printed by Printeria, we have prioritized simplicity over complexity. A more complex model may be more precise, but it requires a large number of parameters whose value is oftenly unknown. Therefore, our models are reduced order but rigorous deterministic models , where their parameters take a concrete, non-probabilistic value.

Constitutive expression models

Constitutive expression models are those in which protein expression is not regulated. The gene that encodes a protein does not depend on any transcription factor, so it will continuously transcribe messenger RNA molecules, and then translation of the protein will be unregulated.

Model design

A simple scheme that summarizes the cellular transcription and translation processes in a constitutive expression model is shown in the following Figure. We only consider as biochemical species involved in reactions to mRNA and our protein of interest (PoI).

Constitutive expression model. Cell schema.

From the cell schema we can deduce the following biochemical reactions.

Constitutive expression model. Biochemical reactions.

Parameter	Description	Units	Value
C_R	Constitutive transcription rate is the transcription rate K_R times the mean plasmid copy number in cell c_n. In our case, we are using the pMBI replication origin, so c_n ∼ 500, and C_R = K_R·c_n	molecules.min^-1	326 [1, 7]
p	mRNA translation rate	min^-1	2.38 [2]
d_m	mRNA degradation rate	min^-1	0.247 [7]
d_p	PoI degradation rate	min^-1	0.156 [5]
μ	Dilution rate	min^-1	0.017 [5]
K_max	Maximum growth capacity	cells	1.6·10⁸ [5]

Constitutive expression model. Model parameters obtained from literature.

With the reactions and approximations already established, we apply the Law of Mass Action kinetics[1] (LMA) to deduce the differential equations. The LMA establishes that the variation of the species resulting from a reaction is proportional to the product of the reactants. In our case, we also take into account an ODE for the cell growth. The resulting ODE model and the main biochemical species are shown below.

Variable	Biochemical species	Units
n₁	mRNA	Molecules
n₂	PoI	Molecules
n₃	Number of cells	Cells

Constitutive expression model. Biochemical species.

Constitutive expression model. Model equations.

After this, a series of quasi-steady state approximations [2] have been made. We have established that mRNA is generated at a constant C_R constitutive transcription rate. In addition, the copy number of plasmids c_n is kept as a constant. We consider that other species such as RNAP polymerases and ribosomes are kept constant as well.

The computational simulation of this ODE model uses two MATLAB files: the mc_simple.m function, which describes the system of differential equations, and the script model_const_simple.m where the parameters are defined and the model is solved by the ode45 MATLAB function. The simulation results are shown in the following Figure.

Constitutive expression model. Model predictions using parameter values from literature.

In the the temporal evolution of the mRNA and the protein PoI we can distinguish two phases: the transient phase and the stationary phase. If we perform different simulations varying some parameters of the model, we will observe how the equilibrium point of the stationary phase varies. MATLAB script mc_sim_analysis.m repeatedly simulates the model by changing the C_R and p parameters. The following Figure shows how an increase of both parameteres implies a greater expression of the protein PoI.

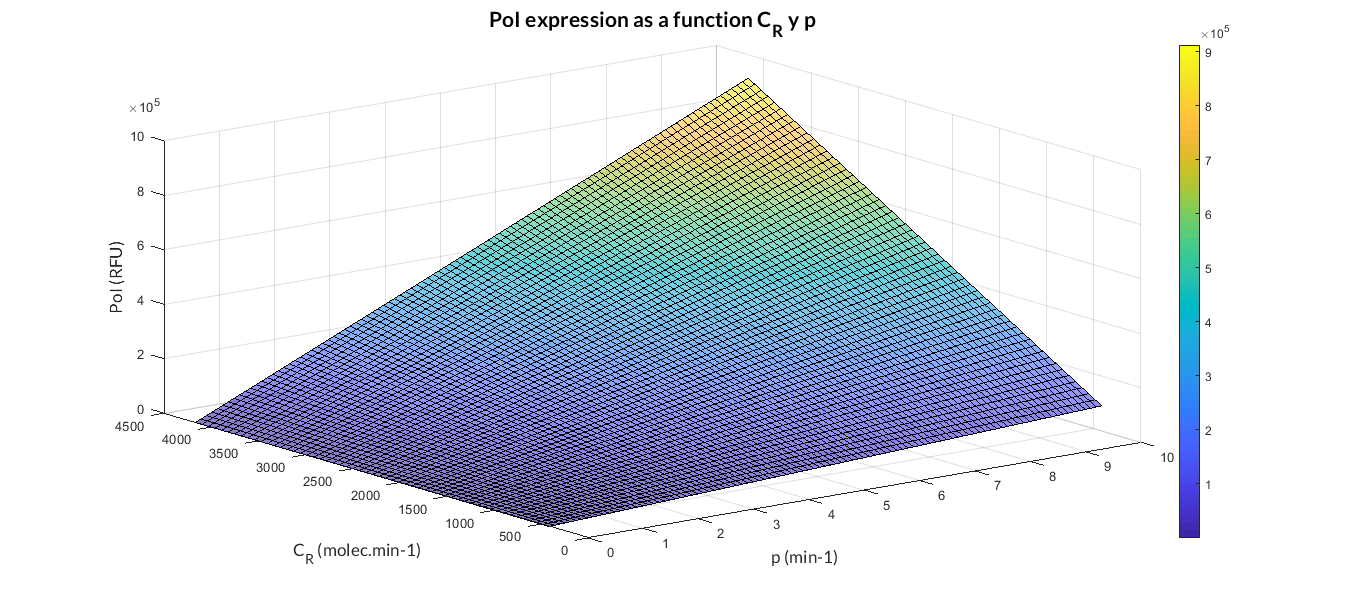
Constitutive expression model analysis. The graph represents de PoI stationary value as function of C_R and p ratios.

At this point anyone could ask us: Which are the advantages of a constitutive expression model like this? Why is a model like this really useful to us? Faced with these questions, the Printeria Modeling team has looked for the answers in the great characteristics that the model offers us.

A simple, easy-to-understand model that clearly explains the processes of cellular transcription and translation.
It is valid for any Printeria construction that has a constitutive expression promoter. The variation between different constructions occurs in the parameters values, not in the model equations!
It has few parameters, with a clear physical meaning, and easily optimizable.
As a compact model, simulations and optimizations are performed at high speed.

Experiments & Optimization

The simple model of constitutive expression is a model that characterizes a large number of Printeria Transcriptional Units (TU), specifically, all those constructions whose promoter is constitutive. We know that all these TU follow the same model, but each one has different parameters, and therefore different experimental values of fluorescence and absorbance. Faced with this situation, the Printeria Lab and Modeling teams have designed some experiments, in which we have applied the multi-objective parameter optimization, and thus check whether the designed constitutive expression model responds to experimental reality.

Experiments changing RBS

We have designed two experiments following the same experimental protocol to assemble different Printeria TUs with the same promoter, CDS (sfGFP reporter protein) and transcriptional terminator, but with different RBSs. Once a TU is made, we estimated the model parameters and particularly the RBS of every TU using the multiobjective optimization protocol.

Printeria TU:

Strong expression: BBa_K2656101.
Medium expression: BBa_K2656103.
Weak expression: BBa_K2656102.
Very weak expression: BBa_K2656100, BBa_K2656104.

Printeria RBS:

Strong expression: BBa_K2656009.
Medium expression: BBa_K2656011.
Weak expression: BBa_K2656010.
Very weak expression: BBa_K2656008, BBa_K2656012.

Experiment parameters	Description
Time	06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)
Number of samples	8 samples for each TU colony
Number of medium samples	8 samples of M9 medium
Temperature	37 ºC
Shake	Double Orbital. Continuously
Absorbance. Optical Density (OD) measure	Wavelenght at 600 nm emission
Excitacion wavelength	Wavelenght at 485 nm
Emission wavelength	Wavelenght at 528 nm
Gain (G)	60

Biotek Cytation 3 experimental parameters.

Optimization specifications	Description
Parameters	Constitutive transcription rate C_R: fixed Translation rate p: to optimize PoI degradation rate d_p: to optimize mRNA degradation rate d_m: fixed Dilution rate μ: to optimize Maximum growth capacity K_max: experimental value
Objetives to optimize	For each TU, we set 2 objetives: FOD (Fluorescence per cell) and OD (Absorbance). In each experiment we measured 3 TU, so we are optimizing 6 objectives per experiment
Parameter ranges	Translation rate p: [0.001 - 6] min^-1 PoI degradation rate d_p: [0.0058 - 0.0087] min^-1 Dilution rate μ: [0.0058 - 0.035] min^-1
MATLAB files	spMODEparam.m: it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution. Experiment 1: spMODEparam_exp1sfGFP.m Experiment 2: spMODEparam_exp2sfGFP.m spMODE.m: it contains the Multi-objective Differential Evolution Algorithm with Spherical Pruning, which optimizes parameters for our experimental results (to execute spMODE.m file we need also SphPruning.m file). CostFunction_RBS_RMS_2n.m: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector. levelDiagram.m: plots Pareto front and Pareto set that gives us back the algorithm. execute_RBS_2n.m: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.

Optimization specifications for the experiment.

Experiment 1 changing RBS. Experimental and optimized simulated model data of strong, medium and weak protein expression RBS

Experiment 2 changing RBS. Experimental and optimized simulated model data of strong and very weak protein expression RBS

Experiment 2 changing RBS. Experimental and optimized simulated model data of very weak protein expression RBS

The results above were obtained after an optimization and decision-making process, where one set of the model parameters were selected to simulate the ODE model of every TU. These simulations were compared with the experimental data showing good agreement. The optimized set of model parameters are summarized in the following table.

Optimized parameters

Values

Translation rate p

Experiment 1:

For strong RBS BBa_K2656009: p = 0.2059 min^-1
For medium RBS BBa_K2656011: p = 0.082 min^-1
For weak RBS BBa_K2656010: p = 0.01 min^-1

Experiment 2:

For strong RBS BBa_K2656009: p = 0.9256 min^-1
For very weak RBS BBa_K2656008: p = 0.04089 min^-1
For very weak RBS BBa_K2656012: p = 0.02889 min^-1

PoI degradation rate d_p

Experiment 1: d_p = 0.0058 min^-1

Experiment 2: d_p = 0.00818 min^-1

Dilution rate μ

Experiment 1:

For strong RBS BBa_K2656009: μ = 0.01492 min^-1
For medium RBS BBa_K2656011: μ = 0.01631 min^-1
For weak RBS BBa_K2656010: μ = 0.01641 min^-1

Experiment 2:

For strong RBS BBa_K2656009: μ = 0.01197 min^-1
For very weak RBS BBa_K2656008: μ = 0.01288 min^-1
For very weak RBS BBa_K2656012: μ = 0.0118 min^-1

List of optimized parameters for RBS experiment.

In addition, the Printeria Modeling team has also calculated the relative strength between the different RBS, taking BBa_K2656009 strong RBS as a reference. The relative strength is the quotient between the values of the protein at the equilibrium point and the reference. The characterization of the RBS parts by their relative strength is shown below.

Original BioBrick RBS part	Printeria RBS part	Relative strength	p parameter ratio (p_RBS/p_ref)
BBa_B0030 (Reference part)	BBa_K2656009 (Reference part)	1	1
BBa_B0034	BBa_K2656011	0.371	0.398
BBa_B0032	BBa_K2656010	0.045	0.048
BBa_J61100	BBa_K2656008	0.042	0.044
BBa_J61101	BBa_K2656012	0.031	0.031

Relative strength between different RBS parts.

Experiments changing promoters

We have designed two experiments following the same experimental protocol to assemble different Printeria TUs with the same RBS, CDS (GFP reporter protein) and transcriptional terminator, but with different promoters. Then, following the optimization protocol we have obtained the model parameters and particularly the promoter values.

Printeria TU:

Strong promoters: BBa_K2656106
Medium promoters: BBa_K2656107
Weak promoters: BBa_K2656105

Printeria promoters:

Strong promoters: BBa_K2656005
Medium promoters: BBa_K2656007
Weak promoters: BBa_K2656004

Experiment parameters	Description
Time	06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)
Number of samples	8 samples for each TU colony
Number of medium samples	8 samples of M9 medium
Temperature	37 ºC
Shake	Double Orbital. Continuously
Absorbance. Optical Density (OD) measure	Wavelenght at 600 nm emission
Excitacion wavelength	Wavelenght at 485 nm
Emission wavelength	Wavelenght at 528 nm
Gain (G)	60

Biotek Cytation 3 experimental parameters.

Optimization specifications	Description
Parameters	Constitutive transcription rate C_R: to optimize Translation rate p: fixed PoI degradation rate d_p: to optimize mRNA degradation rate d_m: fixed Dilution rate μ: to optimize Maximum growth capacity K_max: experimental value
Objetives to optimize	For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In each experiment we have measured 3 TU, so we are optimizing 6 objectives per experiment
Parameter ranges	Constitutive transcription rate C_R: 500 x [0.001 - 5] min^-1 PoI degradation rate d_p: [0.0058 - 0.0087] min^-1 Dilution rate μ: [0.0058 - 0.035] min^-1
MATLAB files	spMODEparam.m: it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution. In this experiment, we have used the spMODEparam_exp6GFP.m MATLAB script. spMODE.m: it contains the Multi-objective Differential Evolution Algorithm with Spherical Pruning, which optimizes parameters for our experimental results (to execute spMODE.m file we need also SphPruning.m file). CostFunction_Prom_RMS_2n.m: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector. levelDiagram.m: plots Pareto front and Pareto set that gives us back the algorithm. execute_Prom_2n.m: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.

Optimization specifications for the experiment.

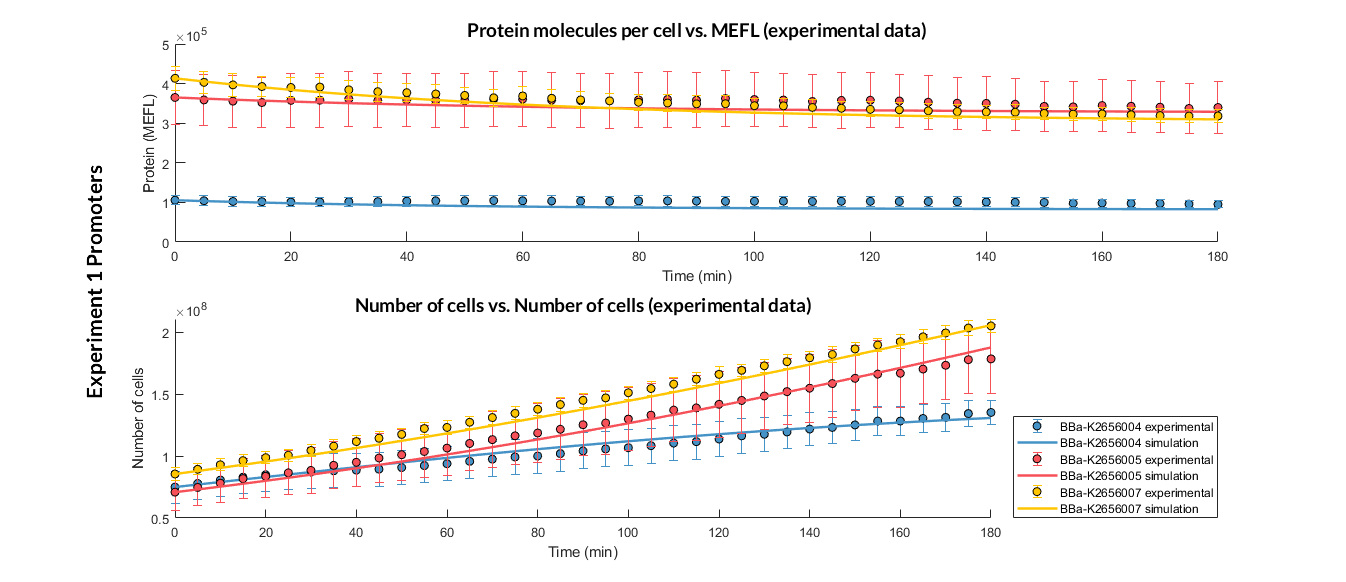
Experiment 1 changing promoters. Experimental and optimized simulated model data of strong, medium and weak promoters.

The results above were obtained after an optimization and decision-making process, where one set of the model parameters were selected to simulate the ODE model of every TU. These simulations were compared with the experimental data showing good agreement.

Optimized parameters	Values
Constitutive transcription rate C_R	For strong promoter BBa_K2656005: C_R = 539.5 min^-1 For medium promoter BBa_K2656007: C_R = 486.25 min^-1 For weak promoter BBa_K2656004: C_R = 171.15 min^-1
PoI degradation rate d_p	d_p = 0.008492 min^-1
Dilution rate μ	For strong promoter BBa_K2656005: μ = 0.0072 min^-1 For medium promoter BBa_K2656007: μ = 0.0068 min^-1 For weak promoter BBa_K2656004: μ = 0.011 min^-1

List of optimized parameters for promoters experiment.

In addition, the Printeria Modeling team has also calculated the relative strength between the different promoters, taking BBa_K2656005 strong promoter as a reference. The characterization of the promoter parts by their relative strength is shown below.

Original BioBrick promoter part	Printeria promoter part	Relative strength	p parameter ratio (p_Prom/p_ref)
BBa_J23102 (Reference part)	BBa_K2656005 (Reference part)	1	1
BBa_J23101	BBa_K2656007	0.9367	0.9013
BBa_J23106	BBa_K2656004	0.2603	0.3172

Relative strength between different promoter parts.

Experiment to compare reporter proteins with and without LVA tag

In the following experiment we want to compare the degradation rate of different protein reporters in two Printeria TUs with identical promoters, RBS and transcriptional terminators. An LVA degradation tag has been added to one of the protein sequences. This tag causes an increase of protease activity, so it means a faster degradation rate of the reporter protein. A priori, the degradation rate in the TU with the LVA tag will be higher.

Printeria TU:

YFP with LVA tag: BBa_K2656111
YFP without LVA tag: BBa_K2656112

Printeria CDS:

YFP with LVA tag: BBa_K2656020
YFP without LVA tag: BBa_K2656021

With these experiments, the team aims:

To analyze the effect of the protein degradation rate variation on our constitutive expression model, and determine if the model fits the experimental results of the reporter proteins with LVA degradation tag.
To characterize the YFP reporter protein with LVA tag as a new iGEM part and as Improve project .

The experiments and optimization process performed for each reporter protein are described below. We have followed the experimental protocol and multi-objective optimization protocol.

YFP with and without LVA tag

Experiment parameters	Description
Time	06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)
Number of samples	8 samples for each TU colony
Number of medium samples	8 samples of M9 medium
Temperature	37 ºC
Shake	Double Orbital. Continuously
Absorbance. Optical Density (OD) measure	Wavelenght at 600 nm emission
Excitacion wavelength	Wavelenght at 500 nm
Emission wavelength	Wavelenght at 540 nm
Gain (G)	60

Biotek Cytation 3 experimental parameters.

Optimization specifications	Description
Parameters	Constitutive transcription rate C_R: fixed Translation rate p: to optimize PoI degradation rate d_p: to optimize mRNA degradation rate d_m: fixed Dilution rate μ: to optimize Maximum growth capacity K_max: experimental value
Objetives to optimize	For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In this experiment we have measured 2 TU, so we are optimizing 4 objectives per experiment
Parameter ranges	Constitutive transcription rate C_R: [0.01 - 2] min^-1 PoI degradation rate d_p: [0.0058 - 0.018] min^-1 Dilution rate μ: [0.0058 - 0.035] min^-1
MATLAB files	spMODEparam.m: it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution. In this experiment, we have used spMODEparam_exp1YFP.m spMODE.m: it contains the Multi-objective Differential Evolution Algorithm with Spherical Pruning, which optimizes parameters for our experimental results (to execute spMODE.m file we need also SphPruning.m file). CostFunction_improve_RMS_2n.m: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector. levelDiagram.m: plots Pareto front and Pareto set that gives us back the algorithm. execute_improve_2n.m: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.

Optimization specifications for the experiment.

After the multiobjective optimization process, we selected one of the solution for the model parameters and then we compared the model simulations with the experimental data. For both TUs, the simulation results match with the experimental ones.

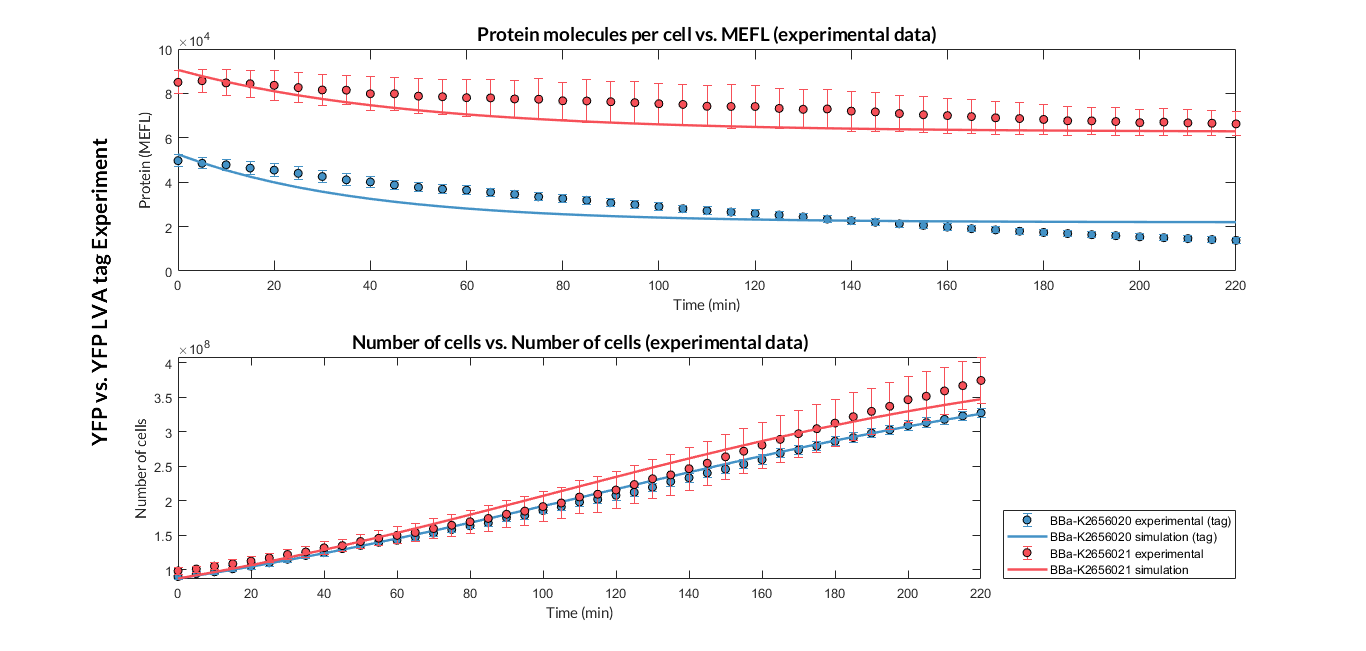
Experiment YFP vs. YFP tag. Experimental data and optimized model of the YFP and YFP tag proteins

Optimized parameters

Values

Translation rate p

For YFP with LVA tag BBa_K2656020: p = 0.4622 min^-1
For YFP without LVA tag BBa_K2656021: p = 1.053 min^-1

PoI degradation rate d_p

For YFP with LVA tag BBa_K2656020: d_p = 0.01492 min^-1
For YFP without LVA tag BBa_K2656021: d_p = 0.0080 min^-1

Dilution rate μ

For YFP with LVA tag BBa_K2656020: μ = 0.01166 min^-1
For YFP without LVA tag BBa_K2656021: μ = 0.01307 min^-1

List of optimized parameters.

At this point, it is easy to see that the degradation rate is significantly higher in the reporter protein with the degradation LVA tag than the YFP protein. Computing the ratio of the degradation rates for both YFP proteins, we observe that the value of the protein with the LVA tag is about twice the value of the protein without LVA tag.

Inducible expression models

Inducible expression models are those where protein expression depends on one or more inducing molecules. They are called activators or repressors. The concentration of these biochemical species determines if the transcription is activated or repressed, respectively.

Our Printeria device gives us the possibility to create some inducible genetic constructs:

P_BAD/araC inducible model
AHL-LuxR inducible model

P_BAD/araC inducible model

The inducible promoter P_BAD/araC [5] is a promoter whose expression depends on two inducing complexes: the L-arabinose (activator) and the araC (repressor). The dimeric protein araC binds DNA to compound a DNA loop and thus prevents the binding between DNA and RNA polymerase. However, when two arabinose molecules bind the araC dimer, the DNA loop is broken and the binding between the RNA polymerase and the promoter region is possible.

We have proposed an ODE model describing the P_BAD/araC mechanism. This theoretical model has been included in the Simulation Tool, so Printeria is able to predict the behavior of the P_BAD/araC inducible promoter circuits.

Model design

We propose the following scheme that describe the biochemical reactions of the P_BAD/araC system. We have assumed a very high concentration of araC inside the cell because the gene encoding for the araC protein is found in the cell genome of some strains (e.g. in DH5α strains).

P_BAD/araC inducible model. Cell schema.

From the cell schema we infer the following biochemical reactions:

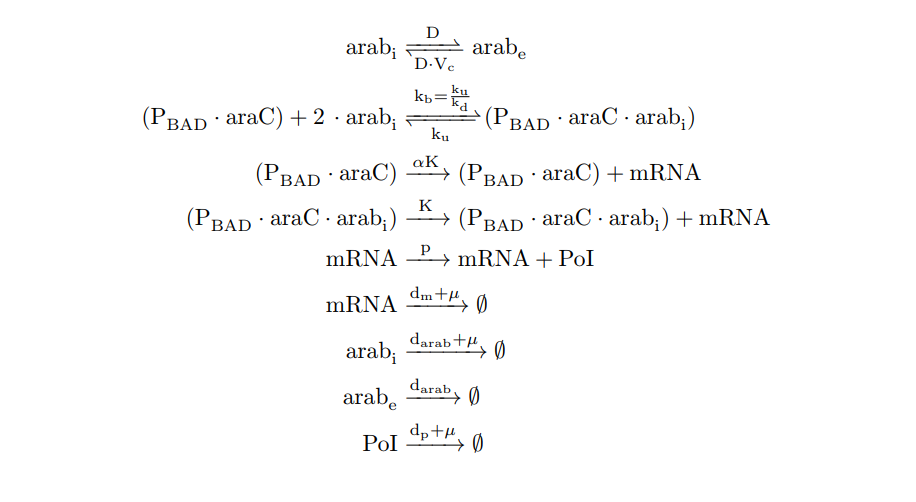
P_BAD/araC inducible model. Biochemical reations.

Parameter	Description	Units	Value
D	Diffusion coefficient	min^-1	2 [2]
V_c	Cell volume(1.1x10^-9 μL)/External volume(1x10^-3 μL)	adimensional	1.1x10^-6 [2]
k_u	Dissociation rate of (P_BAD.araC.arabi) complex	min^-1	10 [10]
k_d	Dissociation constant of (P_BAD.araC.arabi) complex	molec²	100 [2, 10 ]
k_b	Association rate of (P_BAD.araC.arabi) complex. k_u/k_d	molec^-2min^-1	0.1 (Estimated)
K	Transcription rate is the product of transcription rate per plasmid K_t and the mean number of plasmids in cell c_n . In our case, we are using the pMBI replication origin, so c_n ∼ 500, and K = K_t·c_n.	min^-1	326 [1, 7]
α	(P_BAD.araC) basal activity constant	adimensional	0.01 (Estimated)
p	mRNA translation rate	min^-1	2.38 [2]
d_arab	L-arabinose degradation rate. We assume a very slow degradation.	min^-1	∼10^-6
d_m	mRNA degradation rate	min^-1	0.247 [7]
d_p	PoI degradation rate	min^-1	0.0063 [5]
μ	Dilution rate	min^-1	0.017 [5]
K_max	Maximum growth capacity	cells	1.6·10⁸ [5]

P_BAD/araC inducible model. Model parameters.

We apply the Law of Mass Action kynetics (LMA) to obtain the equivalent ODE model. Considerin the same previous assumptions for the constitutive models, and also the fact the the plasmid copy number c_n is kept as a constant, we can obtain a reduced oreder model. Thus, we get a model of six differential equations and one algebraic equation as below.

Variable	Biochemical species	Units
n₁	(P_BAD.araC.arab) complex	Molecules
n₂	Extracellular L-arabinose	Molecules
n₃	Intracellular L-arabinose	Molecules
n₄	mRNA	Molecules
n₅	PoI	Molecules
n₆	Number of cells	Cells

P_BAD/araC inducible model. Biochemical species.

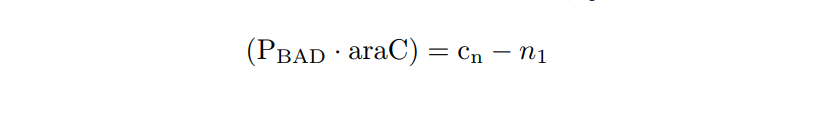
P_BAD/araC inducible model. Model equations.

Now we have two MATLAB files: the mi_araC_simplest.m function, which describes the ODE model, and the script model_inducible_simplest.m where the parameters are defined. The model was simulated by using the ode23t MATLAB function. The simulation results are shown below.

P_BAD/araC inducible model. Model predictions using parameter values from literature.

Once the P_BAD/araC model was validated, we simulated the model varying the some of its parameters (MATLAB script analysis_mi_araC_simplest.m). In this case, we have modified the K transcription rate and the p translation rate.

P_BAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p and K ratios.

As we can see in the 3D graph, the protein expression of PoI exponentially increases when the translation rate p and transcription rate K become higher.

But we can also change the initial concentration of L-arabinose in the P_BAD/araC model as shown in the figure below. The simulations for several p and arab₀ parameters were ran using the analysis_mi_araC_simplest_arab.m MATLAB script.

P_BAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p ratio and L-arabinose concentration (arab₀).

AHL-LuxR inducible model

The AHL-LuxR genetic circuit [2] is a more complex genetic circuit than the models presented so far. It couples two functional subsystems: i) quorum sensing interconnecting cell population with the external inducer AHL, and ii) an intracellular loop to regulate expression of the protein of interest.

The first subsystem implements a cell-to-cell communication mechanism via quorum sensing. It is based on the exchange of the small signaling autoinducer molecule N-acyl-L-homoserine lactone (AHL) to induce population cell consensus. AHL molecules passively diffuses across the cellular membrane from inside the cell to the external environment, and viceversa, following Fick’s Law.

The second subsystem introduces an intracellular loop to control expression of the protein of interest, in this case GFP. First, LuxR protein is expressed by luxR under the constitutive promoter Pc. Then, LuxR and AHL bind forming the heterodimer (LuxR.AHL), which subsequently dimerizes as the heterotetramer transcription factor (LuxR.AHL)₂. The dimer represses protein expression when it is attached to the promoter Plux.

Model design

We propose the following biochemical reactions based on the Boada et al.(2017) model [2].

AHL-LuxR inducible model. Cell schema.

From the schema, we can obtain the following biochemical reactions:

AHL-LuxR inducible model. Biochemical reactions.

Parameter	Description	Units	Value
C_R	Constitutive transcription rate is the transcription rate K_R times the mean plasmid copy number in cell c_n. In our case, we are using the pACYC replication origin, so c_n ∼ 10, and C_R = K_R·c_n	molecules.min^-1	7.9
k_{e_G}	gGFP transcription rate	molecules.min^-1	17.5
α	P_luxR promoter basal activity	adimensional	0.1 (Estimated)
p_R	m_R translation rate	min^-1	10
p_G	m_GFP translation rate	min^-1	3.09
k_A	Synthesis rate of AHL by LuxI	min^-1	0.04
k_-1	Dissociation rate of (R·A)	min^-1	10
k_-2	Dissociation rate of (R·A)₂	min^-1	1
k_d1	Dissociation constant of (R·A)	molecules	100
k_d2	Dissociation constant of (R·A)₂	molecules	20
k_dlux	Dissociation constant of (R·A)₂ to the P_luxR promoter	molecules	10
d_G	GFP degradation rate	min^-1	0.027
d_R	R degradation rate	min^-1	0.2
d_A	A degradation rate	min^-1	0.057
d_{A_e}	A degradation rate in culture medium	min^-1	0.057
d_RA	(R·A) degradation rate	min^-1	0.156
d_RA₂	(R·A)₂ degradation rate	min^-1	0.017
d_{m_R}	m_R degradation rate	min^-1	0.247
D	Diffusion coefficient of AHL through the cell membrane	min^-1	2
V_c	Cell volume(1.1x10^-9 μL)/External volume(1x10^-3 μL)	adimensional	1.1x10^-6
N	Number of cells	cells	240

AHL-LuxR inducible model. Model parameters.

Applying the Law of Mass Action kynetics (LMA) and some quasi-static approximations as before, we can obtain the following ODE model of the AHL-LuxR inducible system.

Variable	Biochemical species	Units
n₁	GFP protein	Molecules
n₂	LuxR protein	Molecules
n₃	Dimer of (R.A)₂	Molecules
n₄	AHL intracellular inducer	Molecules
n₅	AHL_ext intracellular inducer	Molecules
n₆	Monomer (R.A)	Molecules

AHL-LuxR inducible model. Biochemical species.

AHL-LuxR inducible model. Model equations.

As we can see, the model has five differential equations plus one algebraic equation. This model does not describe cell growth, but it considers a constant number of cells N. This is because the measurements were taken in a bioreactor that has one influx with medium similiar to another efflux which washes the cells away. Both fluxes are proportional to the dilution rate, so the cell density is kept constant.

We have programmed a MATLAB function called mi_lux.m for the ODE model, and also a MATLAB script called model_lux.m to define the parameters and simulate the model (ode15s MATLAB function).

AHL-LuxR inducible model. Model predictions using parameter values from literature.

AHL-LuxR inducible model analysis. The graph shows the relation between AHL concentration and protein expression.

As we can see, the results show a clear dependence between the expression of the protein and the inducing AHL concentration. Comparing the experimental data (normalized for different AHL concentrations) with the simulated results, we can see that both closely match and this dynamics is the so-called Hill function.

Multi-objective parameter optimization

To what extent is our model valid? What values should the parameters take? To what extent do the theoretical results resemble the experimental ones? Is our model able to explain the behaviour of cells in reality?

One of the most important phases in the field of Printeria Modeling has been the validation of theoretical models with experimental data. In the Printeria team we wanted to confirm that the models designed are consistent with our experiments. However, we know that the parameters will not take a fixed value, but vary depending on the genetic construction with which we experiment. With this idea in mind, the need to apply an optimization process arises.

The multiobjective parameter optimization process [3] minimizes two or more design objectives that have a trade-off between them. They are cost functions that depend on some decision variables. In our case, these objectives are estimation errors between experimental data and the model predictions, whereas the decission variables are some of our model parameters. Using a mathematical algorithm to perform multiobjective optimization, we can find the optimal solutions for the model parameters also known as Pareto Front. The Pareto front has the optimal solutions that do not improve one objective without worsening the remaining objectives.

In multi-objective optimization, there is no single solution, but rather a set of them which form the Pareto front. For each of these solutions, we find a set of decision variables: the Pareto set [6]. In our case, the Pareto front solutions represent the RMS error between experimental data and model predictions, and the Pareto set has the sets of parameters associated to one Pareto front solution.

The Printeria Modeling team has established a protocol to obtain the optimal solutions of the model parameters for any experiment:

We define the objectives to be optimized. These will be the values of Fluorescence F/Unit of Absorbance OD or FOD, and the cellular growth (OD) of a Transcriptional Unit (TU). Therefore, if we have different n TU in an experiment, we will optimize 2n objectives.
We choose the parameters to optimize and establish the range of values they can take.
We select the identification and validation data. The identification data are those used in the optimization process. The validation data are used to compare the experiment with the simulated theoretical model and the optimized parameters.
We define the cost function, which specifies the error function to be minimized. It simulates the model for different parameter values, and calculates the error between the simulation data and the experimental identification data.
The mathematical optimization algorithm is executed. In our case we use the Multi-objective Differential Evolution Algorithm with Spherical Pruning. This algorithm uses the cost function to test different parameter values and thus search for optimal parameter values.
The Pareto set and Pareto front diagrams and the different solutions of our optimized parameters for the different objectives are obtained.
Decision Making is carried out by the designer. The optimal parameters are chosen for our 2n objectives.
The model is simulated with the optimized parameters and compared with the validation data.

Following this protocol for each experiment, we have determined the best parameters for our models that fully fit the experimental data.

Simulation Tool

One of the main challenges of Printeria has been to give the user a chance to really understand what our device is doing when it prints genetic circuits on bacteria. So we have also sought to provide as much information as possible about the Printeria product. And what better way than to give our user a quantitative, mathematical description of what happens in our cells?

In our project we believe that mathematical modeling can be a very powerful tool for transmitting knowledge, so the Printeria Software and Modeling teams have brought together the most outstanding mathematical models in a single Simulation Tool.

Our Simulation Tool has been conceived as a mathematical model simulation program that has been perfectly integrated into our Printeria Controller software. When our user wants to assemble a genetic construct and selects the parts, the Simulation Tool offers the possibility to experiment in silico and predict cell behavior before printing the bacteria. All this, just by pressing the Show model results button... and instantly!

But how does the Simulation Tool work?

The Printeria Modeling and Software teams have jointly designed a program developed in a single Python script (have a look at our simulate.py script). The program combines the functions of the main mathematical models of Printeria with the information of the Printeria kit stored in the Printeria database. In addition, as it is a single Python file, it is stored and run on the Raspberry Pi 3 server.

Now let's see what happens if the user has chosen the Printeria parts and presses the Simulate button...

Simulation Tool working scheme.

The Printeria client connects to the Printeria database (MongoDB) where we store all the information of our Printeria kit.
The four parts of the genetic construction (promoter, RBS, CDS and transcriptional terminator) are extracted from the database thanks to their identifiers.
The type of model (constitutive or inducible expression) is identified from the type of promoter selected.
The model parameters of each construction part are extracted.
The initial conditions of the simulation and its duration are established.
The model is simulated using Python's odeint function
A temporary CSV file is generated in which the we store the results of the simulation in a certain format.
From the CSV file, the simulation results are represented graphically on the Printeria site. The user can view or download their results.

And what are the advantages of an application like our Simulation Tool?

User-friendly. It is very simple to operate for the user. Just select your Printeria parts, press a button... And that's it!
Integrated. All our software is included in the Raspberry Pi 3 server. You don't need to download the program.
Instant experimental data. Our Simulation Tool runs simulations at high speed. In a few seconds you'll have your results.
Customizable parameters. You can modify your parameters and adapt them to your experiment, to obtain more precise results.
All-in-one. Our Simulation Tool includes several mathematical models, constitutive and inducible, in a single code and solves them particularizing for each Printeria genetic construction.

Would you like to try the Simulation Tool? Go to our Printeria Controller site and discover all the possibilities offered by our software.

What are you waiting for to start discovering it?

References

Picó, J., Vignoni, A., Picó-Marco, E., & Boada, Y. (2015). Modelado de sistemas bioquímicos: De la ley de acción de masas a la aproximación lineal del ruido. Revista Iberoamericana de Automática e Informática Industrial RIAI, 12(3), 241-252.
Y. Boada, A. Vignoni, and J. Picó. (2017). Engineered control of genetic variability reveals interplay among quorum sensing, feedback regulation, and biochemical noise. ACS Synthetic Biology, 6(10):1903–1912, 2017a.
Segel, L. A., & Slemrod, M. (1989). The quasi-steady-state assumption: a case study in perturbation. SIAM review, 31(3), 446-477.
Boada, Y., Vignoni, A., Reynoso-Meza, G., & Picó, J. (2016). Parameter identification in synthetic biological circuits using multi-objective optimization. Ifac-Papersonline, 49(26), 77-82.
R. Milo and R. Phillips. Cell Biology by the Numbers. First edition, 2015. ISBN9780815345374.
Boada, Y., Vignoni, A., & Picó, J. (2017). Reduction of population variability in protein expression: A control engineering approach. Actas de las XXXVIII Jornadas de Automática.
U. Alon. An Introduction to Systems Biology. Desing Principles of Biological Circuits. Champan and Hall/CRC, Edition, 2007.
Schleif, R. (2000). Regulation of the L-arabinose operon of Escherichia coli. Trends in Genetics, 16(12), 559-565.
Boada, Y. (2018). A systems engineering approach to model, tune and test synthetic gene circuits. PhD. Thesis, Universitat Politècnica de València.
N. E. Buchler, U. Gerland, and T. Hwa. Nonlinear protein degradation and the function of genetic circuits. Proceedings of the National Academy of Sciences of the United States of America, 102(27):9559–9564, 2005.

[1] Picó, J., Vignoni, A., Picó-Marco, E., & Boada, Y. (2015). Modelado de sistemas bioquímicos: De la ley de acción de masas a la aproximación lineal del ruido. Revista Iberoamericana de Automática e Informática Industrial RIAI, 12(3), 241-252.

[2] Y. Boada, A. Vignoni, and J. Picó. (2017). Engineered control of genetic variability reveals interplay among quorum sensing, feedback regulation, and biochemical noise. ACS Synthetic Biology, 6(10):1903–1912, 2017a.

[3] Segel, L. A., & Slemrod, M. (1989). The quasi-steady-state assumption: a case study in perturbation. SIAM review, 31(3), 446-477.

[4] Boada, Y., Vignoni, A., Reynoso-Meza, G., & Picó, J. (2016). Parameter identification in synthetic biological circuits using multi-objective optimization. Ifac-Papersonline, 49(26), 77-82.

[5] R. Milo and R. Phillips. Cell Biology by the Numbers. First edition, 2015. ISBN9780815345374.

[6] Boada, Y., Vignoni, A., & Picó, J. (2017). Reduction of population variability in protein expression: A control engineering approach. Actas de las XXXVIII Jornadas de Automática.

[7] U. Alon. An Introduction to Systems Biology. Desing Principles of Biological Circuits. Champan and Hall/CRC, Edition, 2007.

[8] Schleif, R. (2000). Regulation of the L-arabinose operon of Escherichia coli. Trends in Genetics, 16(12), 559-565.

[9] Boada, Y. (2018). A systems engineering approach to model, tune and test synthetic gene circuits. PhD. Thesis, Universitat Politècnica de València.

[10] N. E. Buchler, U. Gerland, and T. Hwa. Nonlinear protein degradation and the function of genetic circuits. Proceedings of the National Academy of Sciences of the United States of America, 102(27):9559–9564, 2005.

@@ Line 49: / Line 49: @@
 <div class="main-container">
-             <section style="/* background-color: #353535; *//* background-image: url(&quot;https://previews.123rf.com/images/bogdanhoda/bogdanhoda1504/bogdanhoda150400014/38730978-test-tubes-in-clinic-pharmacy-and-medical-research-laboratory-with-male-scientist-using-pipette.jpg&quot;); *//* background-size: 100%; */height:44.2em;margin-top: 0em;padding-top: 1.1em;" class="height-90 parallax">
+             <section style="
-               <div class="main-container" style="
+; ; background-size: 100%;height: 44.2em;margin-top: 0em;padding-top: 1.1em;" class="height-90 parallax">
+<div class="main-container" style="
 height: 100%;">
-               <center style="
+<center style="
 height: 100%;">
-               <div class="col-md-10" style="
+<div class="col-md-10" style="
-height: 100%;margin-top: 4em;">
+  height: 100%;margin-top: 4em;">
-<div id="logoPrinteria" class="item" style="
+  <div id="logoPrinteria" class="item" style="
-background-image: url(http://via.placeholder.com/1155x666);
+    background-image: url(https://static.igem.org/mediawiki/2018/thumb/b/b2/T--Valencia_UPV--ModelFondoUPV2018.jpeg/1200px-T--Valencia_UPV--ModelFondoUPV2018.jpeg);
-height: 100%;
+    height: 100%;
-width: 100%;background-attachment: fixed; background-position: center; background-position-y: 100px; background-repeat: no-repeat">
+    width: 100%;background-attachment: fixed;background-size: cover;"><img src="https://static.igem.org/mediawiki/2018/thumb/2/2c/T--Valencia_UPV--ModelTextoUPV2018.jpeg/1200px-T--Valencia_UPV--ModelTextoUPV2018.jpeg.png" style=" margin-top: 0px;">
+      <a class="btn down inner-link active" href="#story" style="font-size: 82%;right: 50%;/* position: fixed; *//* bottom: 7%; */top: 85.2%;z-index: 99;background-color: white;position: absolute;border-radius: 80%;width: 3.8em;height: 3.8em;padding: 0;padding-top: 14px;">
-    <div style="/* position: absolute; *//* top: 81%; *//* padding-left: 31em; */">
+        <i class="stack-interface stack-down-open-big"></i>
-<a class="btn down inner-link active" href="#story" style="font-size: 82%;/* position: fixed; *//* bottom: 7%; */top: 541px;z-index: 99;background-color: white;position: relative;border-radius: 80%;width: 3.8em;height: 3.8em;padding: 0;padding-top: 14px;">
+      </a>
-            <i class="stack-interface stack-down-open-big"></i>
+    </div>
-        </a>
 </div>
+</center>
- </div>
+</div><div class="all-page-modals"></div><div class="all-page-modals"></div>
+<div class="all-page-modals"></div>
+</section>
 </div>
-               </center>
-</div>
-              </section></div>
 <a class="anchorOffset" id="story"></a>
 <section class="feature-large" style="padding-top: 6em; padding-bottom: 50px; outline: none;" data-scroll-id="story" tabindex="-1">
@@ Line 98: / Line 92: @@
                             opacity: 1;
                             ">Models & Experiments</a>
-                           <!--<ul style="list-style-type: circle;">
-                           	<li><p>
-                           		<a href="#design_process" class="lateral inner-link" style="
-		                           color: #353535;
-		                           opacity: 1;
-		                           ">Modeling process</a>
-                           	</p></li>
-                           	<li><p>
-                           		<a href="#const_models" class="lateral inner-link" style="
-		                           color: #353535;
-		                           opacity: 1;
-		                           ">Constitutive expression models</a>
-                           	</p></li>
-                           	<li><p>
-                           		<a href="#ind_models" class="lateral inner-link" style="
-		                           color: #353535;
-		                           opacity: 1;
-		                           ">Inducible expression models</a>
-                           	</p></li>
-                           	<li><p>
-                           		<a href="#optimization" class="lateral inner-link" style="
-		                           color: #353535;
-		                           opacity: 1;
-		                           ">Multi-objective parameter optimization</a>
-                           	</p></li>
-                           </ul>-->
                       </div>
                    </li>
@@ Line 154: / Line 123: @@
              <div>
                 <a class="anchorOffset" id="lmModeling"></a>
-                <h2 class="h2Modeling">Modeling</h2>
                 <p>
-               	<b>Do you think it is possible to mathematically describe a cell? Would you like to know the possibilities that modeling offers you?</b>
+                <b>Do you think it is possible to mathematically describe a cell? Would you like to know the possibilities that modeling offers you?</b>
-               	</p>
-               	<p>
-				One of the fundamental bases of the Printeria project has undoubtedly been <b>mathematical modeling</b>. Thanks to the development and application of new mathematical models, it is possible to <b>quantify the expression of proteins</b> in cells, and therefore <b>characterize</b> through different experiments the parts designed by Printeria. From the Printeria Modeling team, we intend to reach different goals:
-				</p>
-				<ul>
-				<li><p>
-					<b>Design simple mathematical models</b> based on differential equations that describe the biochemical processes of a cell. With them, we can simulate the different genetic circuits that Printeria allows us to build.
-				</p></li>
-				<li><p>
-					Develop a <b>Simulation Tool</b> that allows the user to visualize a prediction of the results of their experiment before running it in Printeria.
-				</p></li>
-				<li><p>
-					<b>Optimize model parameters</b> to match simulation results to experimental data obtained from Printeria constructions.
-				</p></li>
-				<li><p>
-					<b><a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#imCharact" target="_blank">Characterize the parts</a>of our <a href="https://2018.igem.org/Team:Valencia_UPV/Part_Collection" target="_blank">Part Collection</a></b> from the optimization results and provide the user with all the information about the Printeria kit.
-				</p></li>
-				</ul>
-				<p>
-				Although in the development of the project we have dealt with all these aspects, all of them have a single purpose: demonstrate the importance and many applications of <b>describing in a mathematical way the biological processes</b> that take place inside the cell.
                  </p>
-               <!--BOTONES PARA MOVERSE POR LA PÁGINA -->
+                <p>
-               <!--Los enlaces están bien pero los ids a donde apuntan están descuadrados adrede para que al pulsar lleve un poco por encima del contenido -->
+        One of the fundamental bases of Printeria has undoubtedly been <b>mathematical modeling</b>. Thanks to the development and application of new mathematical models, it is possible to <b>quantify the expression of proteins</b> in cells, and therefore <b>characterize</b> through different experiments the parts designed by Printeria. From the Printeria Modeling team, we intend to reach different goals:
-               <div id="" data-scroll-id="" tabindex="-1" style="outline: none;margin-top: 1em;margin-bottom: 1em;justify-content: center;" class="row">
+        </p>
-                  <div class="col-md-3" style="text-align: center;margin-right: 2em;">
+        <ul>
-                     <a class="inner-link" href="#models"><img class="fotosModeling" src="https://static.igem.org/mediawiki/2018/c/ca/T--Valencia_UPV--instagramUPV2018.png"></a>
+        <li><p>
-                     <p style="text-align: center !important; font-weight: bold;">Models &amp; Experiments</p>
+          <b>Design simple mathematical models</b> based on differential equations that describe the biochemical processes of a cell. With them, we can simulate the different genetic circuits that Printeria allows us to build.
-                  </div>
+        </p></li>
-                  <div class="col-md-3" style="text-align: center;margin-right: 2em;">
+        <li><p>
-                     <a class="inner-link" href="#simtool"><img class="fotosModeling" src="https://static.igem.org/mediawiki/2018/c/ca/T--Valencia_UPV--instagramUPV2018.png"></a>
+          Develop a <b>Simulation Tool</b> that allows the user to visualize a prediction of the results of their experiment before running it in Printeria.
-                     <p style="text-align: center !important; font-weight: bold;">Simulation Tool</p>
+        </p></li>
-                  </div>
+        <li><p>
-               </div>
+          <b>Optimize model parameters</b> to match simulation results to experimental data obtained from Printeria constructions.
-               <!--FIN BOTONES PARA MOVERSE POR LA PÁGINA -->
+        </p></li>
+        <li><p>
+          <b><a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#imCharact" target="_blank">Characterize the parts</a> of our <a href="https://2018.igem.org/Team:Valencia_UPV/Part_Collection" target="_blank">Part Collection</a></b> from the optimization results and provide the user with all the information about the Printeria kit.
+        </p></li>
+        </ul>
+        <p>
+        Although in the development of the project we have dealt with all these aspects, all of them have a single purpose: demonstrate the importance and many applications of <b>describing in a mathematical way the biological processes</b> that take place inside the cell.
+                </p>
                 <div>
-               	<a class="anchorOffset" id="models"></a>
+                <a class="anchorOffset" id="models"></a>
                    <h3>Models & Experiments</h3>
                      <p><a href=""></a>
-                     The development of <b>new and simple mathematical models</b> has been one of the essential bases of the Printeria project. The models offer us a <b>multitude of applications</b>: to describe the basic biochemical reactions of the cell, to <a href="#charact" class="inner-link">characterize</a> the parts of our Printeria kit by means of different experiments or to elaborate <a href="#simtool" class="inner-link">new tools</a> that facilitate to our user the learning of Synthetic Biology.
+                     The development of <b>new and simple mathematical models</b> has been one of the essential bases of the Printeria project. The ODE models offer a <b>multitude of applications</b>: describing the basic biochemical reactions of the cell, to <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#imCharact" class="inner-link">characterizing</a> the parts of our Printeria kit by means of different experiments, and elaborating <a href="#simtool" class="inner-link">new tools</a> that facilitate the user learn about Synthetic Biology.
                      </p>
                      <p>
-                     In Printeria Modeling team, we have grouped the models designed in <b>two fields</b>: <a href="#const_models" class="inner-link"><b>constitutive expression models</b></a> and <a href="#ind_models" class="inner-link"><b>inducible expression models</b></a>. We have also established an <a href="#https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" class="inner-link"><b>experimental protocol</b></a> and a <a href="#optimization" class="inner-link"><b>multi-objective optimization protocol</b></a> in order to contrast theoretical and experimental results. With them, we can describe practically all the cells modified with Printeria.
+                     In Printeria Modeling team, we have grouped the models designed in <b>two fields</b>: <a href="#const_models" class="inner-link"><b>constitutive expression models</b></a> and <a href="#ind_models" class="inner-link"><b>inducible expression models</b></a>. We have also established an <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" target="_blank"><b>experimental protocol</b></a> and a <a href="#optimization" class="inner-link"><b>multi-objective optimization protocol</b></a> in order to contrast theoretical and experimental results. With them, we can describe practically all the cells modified with Printeria.
                      </p>
                      <p align="center">
-                    	<b>Want to find out more about how we did it?</b>
+                      <b>Want to find out more about how we did it?</b>
                      </p>
@@ Line 217: / Line 165: @@
                      <h4>Modeling process</h4>
                      <p>
-                     At the beginning of the design of any mathematical model, we have started from a <b>cell scheme</b> in which all the <b>cellular biochemical reactions</b> we wish to model are represented. From the reactions, a set of equations is deduced. Each of these equations describes the <b>temporal variation of the biochemical species</b> in the cell (DNA, RNA, proteins...), and depends on a set of <b>parameters with a physical meaning</b>.
+                     At the beginning of the design of any mathematical model, we have started from a <b>cell scheme</b> in which all the <b>biochemical reactions</b> happen. From the reactions, a set of equations is inferred. Each of these equations describe the <b>temporal evolution of the main biochemical species</b> in the cell (DNA, RNA, proteins and transcription factors), and depend on a set of <b>parameters with a physical meaning</b>.
                      </p>
                      <a href="https://static.igem.org/mediawiki/2018/7/7e/T--Valencia_UPV--esq_modelingUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/7/7e/T--Valencia_UPV--esq_modelingUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/7/7e/T--Valencia_UPV--esq_modelingUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Modeling process schema.</h6>
                      <p>
-                     Because they are <b>differential and generally non-linear equations</b>, mathematical models are simulated using software tools such as MATLAB. The results obtained from the <b>simulation</b> reflect the evolution of the <b>concentration of biochemical species over time</b>. These theoretical results can be contrasted with the experimental data obtained in the laboratory and and thereby adjust the parameters so that the model adapts to the data in an optimal way. This process, called <b>multiobjective parameter optimization</b>, is the process that allows us to <b>validate our models</b> and see if they respond to what happens inside the cells.
+                     Because they are <b> ordinary differential and generally non-linear equations (ODE)</b>, mathematical models are simulated using software tools such as MATLAB. The results obtained from the <b>simulation</b> reflect the evolution of the <b>concentration of biochemical species over time</b>. These theoretical results can be contrasted with the experimental data obtained in the laboratory and thereby adjust the parameters. The ODE model fits the data in an optimal way. This process, called <b>multiobjective parameter optimization</b>, is the process that allows us to <b>validate our models</b> and see if they respond to what happens inside the cells.
                      </p>
                      <p>
-                     In the development of the set of mathematical models that describe the genetic circuits printed by Printeria, we have prioritized <b>simplicity over complexity</b> of the model. A more complex model may be more precise, but it requires a large number of parameters whose value is often unknown. Therefore, our models are composed of <b>few equations and parameters</b>, and they are all <b>deterministic models</b>, that is, their parameters take a concrete, non-probabilistic value.
+                     The development of the set of mathematical models of the genetic circuits printed by Printeria, we have prioritized <b>simplicity over complexity</b>. A more complex model may be more precise, but it requires a large number of parameters whose value is oftenly unknown. Therefore, our models are <b> reduced order but rigorous deterministic models </b>, where their parameters take a concrete, non-probabilistic value.
                      </p>
@@ Line 234: / Line 183: @@
                      <h4>Constitutive expression models</h4>
                      <p>
-                     Constitutive expression models are those in which the expression of the <b>cell's messenger RNA (mRNA) is not regulated</b>. The gene does not depend on any inducing biochemical species, so it will produce RNA molecules continuously, and therefore the translation of the protein will also be constant.
+                     Constitutive expression models are those in which protein expression is not regulated. The gene that encodes a protein does not depend on any transcription factor, so it will  continuously transcribe messenger RNA molecules, and then translation of the protein will be unregulated.
                      </p>
                      <h5><i>Model design</i></h5>
@@ Line 242: / Line 191: @@
                      <a href="https://static.igem.org/mediawiki/2018/5/54/T--Valencia_UPV--const_schemaUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/5/54/T--Valencia_UPV--const_schemaUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/5/54/T--Valencia_UPV--const_schemaUPV2018.png" />
-					</a>
+          </a>
+                     <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Cell schema.</h6>
                      <p>
                      From the cell schema we can deduce the following biochemical reactions.
                      </p>
                      <a href="https://static.igem.org/mediawiki/2018/0/08/T--Valencia_UPV--react_constUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/0/08/T--Valencia_UPV--react_constUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/0/08/T--Valencia_UPV--react_constUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Biochemical reactions.</h6>
                      <table style="width:100%">
-						<tr>
+            <tr>
-						  <th><p>Parameter</p></th>
+              <th><p>Parameter</p></th>
-						  <th><p>Description</p></th>
+              <th><p>Description</p></th>
-						  <th><p>Units</p></th>
+              <th><p>Units</p></th>
-						  <th><p>Value</p></th>
+              <th><p>Value</p></th>
-						</tr>
+            </tr>
-						<tr>
+             <tr>
-						  <td><p>C<sub>R</sub></p></td>
+              <td><p>C<sub>R</sub></p></td>
-						  <td><p>Constitutive transcription rate is calculated by multiplying the transcription rate per plasmid K<sub>R</sub> by the mean plasmids copy number in cell c<sub>n</sub> . In our case, we are using the pMBI replication origin, so c<sub>n</sub> <meta charset="utf-8">&sim; 500, and C<sub>R</sub> = K<sub>R</sub>·c<sub>n</sub>.</p></td>
+              <td><p>Constitutive transcription rate is the transcription rate K<sub>R</sub> times the mean plasmid copy number in cell c<sub>n</sub>. In our case, we are using the pMBI replication origin, so c<sub>n</sub> <meta charset="utf-8">&sim; 500, and C<sub>R</sub> = K<sub>R</sub>·c<sub>n</sub></p></td>
-						  <td><p>molecules.min<sup>-1</sup></p></td>
+              <td><p>molecules.min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>326 [<a href="#references1" class="inner-link">1</a>, <a href="#references7" class="inner-link">7</a>]</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>p</p></td>
+              <td><p>p</p></td>
-						  <td><p>Translation rate</p></td>
+              <td><p>mRNA translation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
+              <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>2.38 [<a href="#references2" class="inner-link">2</a>]</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>d<sub>m</sub></p></td>
+              <td><p>d<sub>m</sub></p></td>
-						  <td><p>mRNA degradation rate</p></td>
+              <td><p>mRNA degradation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
+              <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>0.247 [<a href="#references7" class="inner-link">7</a>]</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>d<sub>p</sub></p></td>
+              <td><p>d<sub>p</sub></p></td>
-						  <td><p>PoI degradation rate</p></td>
+              <td><p>PoI degradation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
+              <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>0.156 [<a href="#references5" class="inner-link">5</a>]</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p><meta charset="utf-8">&mu;</p></td>
+              <td><p><meta charset="utf-8">&mu;</p></td>
-						  <td><p>Dilution rate</p></td>
+              <td><p>Dilution rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
+              <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>0.017 [<a href="#references5" class="inner-link">5</a>]</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>K<sub>max</sub></p></td>
+              <td><p>K<sub>max</sub></p></td>
-						  <td><p>Maximum growth capacity</p></td>
+              <td><p>Maximum growth capacity</p></td>
-						  <td><p>cells</p></td>
+              <td><p>cells</p></td>
-						  <td><p><a href="">---</a></p></td>
+              <td><p>1.6·10<sup>8</sup> [<a href="#references5" class="inner-link">5</a>]</p></td>
-						 </tr>
+             </tr>
-					</table>
+          </table>
-					<a id="LMA" class="anchorOffset"></a>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Model parameters obtained from literature.</h6>
+          <a id="LMA" class="anchorOffset"></a>
                      <p>
-                     With the reactions and approximations already established, we apply the <b>Law of Mass Action kynetics</b>[<a href="#references" class="inner-link">1</a>] (LMA) to deduce the differential equations. The LMA establishes that the variation of the species resulting from a reaction is proportional to the product of the reactants. In our case, to the set of differential equations deduced from the reactions we add a cell growth equation. Biochemical species and our model of equations obtained are shown below.
+                     With the reactions and approximations already established, we apply the <b>Law of Mass Action kinetics</b>[<a href="#references" class="inner-link">1</a>] (LMA) to deduce the differential equations. The LMA establishes that the variation of the species resulting from a reaction is proportional to the product of the reactants. In our case, we also take into account an ODE for the cell growth. The resulting ODE model and the main biochemical species are shown below.
                      </p>
                      <table style="width:100%">
-						<tr>
+            <tr>
-						  <th><p>Variable</p></th>
+              <th><p>Variable</p></th>
-						  <th><p>Biochemical species</p></th>
+              <th><p>Biochemical species</p></th>
-						  <th><p>Units</p></th>
+              <th><p>Units</p></th>
-						</tr>
+            </tr>
-						 <tr>
+             <tr>
-						  <td><p>n<sub>1</sub></p></td>
+              <td><p>n<sub>1</sub></p></td>
-						  <td><p>mRNA</p></td>
+              <td><p>mRNA</p></td>
-						  <td><p>Molecules</p></td>
+              <td><p>Molecules</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>n<sub>2</sub></p></td>
+              <td><p>n<sub>2</sub></p></td>
-						  <td><p>PoI</p></td>
+              <td><p>PoI</p></td>
-						  <td><p>Molecules</p></td>
+              <td><p>Molecules</p></td>
-						 </tr>
+             </tr>
-						 <tr>
+             <tr>
-						  <td><p>n<sub>3</sub></p></td>
+              <td><p>n<sub>3</sub></p></td>
-						  <td><p>Number of cells</p></td>
+              <td><p>Number of cells</p></td>
-						  <td><p>Cells</p></td>
+              <td><p>Cells</p></td>
-						 </tr>
+             </tr>
-					</table>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Biochemical species.</h6>
-					<a href="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--eq_constUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--eq_constUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--eq_constUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--eq_constUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Model equations.</h6>
                      <p>
-                     By obtaining the equations, and seeking the simplicity of the model, a series of <b>quasi-steady state approximations</b> [<a href="#references" class="inner-link">2</a>] have been made. We have established that mRNA is generated with a constant C<sub>R</sub> constitutive transcription rate. Another consideration has been to assume that the copy number of plasmids c<sub>n</sub> in cell is a constant. We have also proposed that other species such as ribosomes, which also participate in transcription, are constant over time.
+                     After this, a series of <b>quasi-steady state approximations</b> [<a href="#references" class="inner-link">2</a>] have been made. We have established that mRNA is generated at a constant C<sub>R</sub> constitutive transcription rate. In addition, the copy number of plasmids c<sub>n</sub> is kept as a constant. We consider that other species such as RNAP polymerases and ribosomes are kept constant as well.
                      </p>
                      <p>
-                     After developing the model and raising the reactions and equations, two files have been programmed in MATLAB: the <a href="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--mc_simpleUPV2018.txt" target="_blank">mc_simple.m</a> function, which describes the system of differential equations, and the script <a href="https://static.igem.org/mediawiki/2018/4/4e/T--Valencia_UPV--model_const_simpleUPV2018.txt" target="_blank">model_const_simple.m</a> in which the parameters are defined and the model is solved by the <a href="https://es.mathworks.com/help/matlab/ref/ode45.html?searchHighlight=ode45&s_tid=doc_srchtitle" style="padding-right: 0" target="_blank">ode45</a> MATLAB function. The result of the simulation of the model is shown in the following Figure.
+                     The computational simulation of this ODE model uses two  MATLAB files: the <a href="https://static.igem.org/mediawiki/2018/e/e1/T--Valencia_UPV--mc_simpleUPV2018.txt" target="_blank">mc_simple.m</a> function, which describes the system of differential equations, and the script <a href="https://static.igem.org/mediawiki/2018/4/4e/T--Valencia_UPV--model_const_simpleUPV2018.txt" target="_blank">model_const_simple.m</a> where the parameters are defined and the model is solved by the <a href="https://es.mathworks.com/help/matlab/ref/ode45.html?searchHighlight=ode45&s_tid=doc_srchtitle" style="padding-right: 0" target="_blank">ode45</a> MATLAB function. The simulation results are shown in the following Figure.
-                	</p>
+                  </p>
-                	<a href="https://static.igem.org/mediawiki/2018/f/f1/T--Valencia_UPV--model_const_sim_graphUPV2018.png" data-lightbox="true">
+                  <a href="https://static.igem.org/mediawiki/2018/f/f1/T--Valencia_UPV--model_const_sim_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/f/f1/T--Valencia_UPV--model_const_sim_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/f/f1/T--Valencia_UPV--model_const_sim_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model. Model predictions using parameter values from literature.</h6>
                      <p>
-                     In the simulation of mRNA and PoI we distinguish two phases in the temporal evolution of the species: the transient phase and the stationary phase. If we perform different simulations varying some parameters of the model, we can observe how the equilibrium value of the stationary phase varies. MATLAB script <a href="https://static.igem.org/mediawiki/2018/4/4d/T--Valencia_UPV--mc_sim_analysisUPV2018.txt" target="_blank">mc_sim_analysis.m</a> repeatedly simulates the model by varying the C<sub>R</sub> and p parameters, and graphs the results. The following Figure shows how an increase in both ratios implies a greater expression of the protein.
+                     In the the temporal evolution of the mRNA and the protein PoI we can distinguish two phases: the transient phase and the stationary phase. If we perform different simulations varying some parameters of the model, we will observe how the equilibrium point of the stationary phase varies. MATLAB script <a href="https://static.igem.org/mediawiki/2018/4/4d/T--Valencia_UPV--mc_sim_analysisUPV2018.txt" target="_blank">mc_sim_analysis.m</a> repeatedly simulates the model by changing the C<sub>R</sub> and p parameters. The following Figure shows how an increase of both parameteres implies a greater expression of the protein PoI.
                      </p>
-					<a href="https://static.igem.org/mediawiki/2018/f/f9/T--Valencia_UPV--mc_sim_analysis_graphUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/f/f9/T--Valencia_UPV--mc_sim_analysis_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/f/f9/T--Valencia_UPV--mc_sim_analysis_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/f/f9/T--Valencia_UPV--mc_sim_analysis_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Constitutive expression model analysis. The graph represents de PoI stationary value as function of C<sub>R</sub> and p ratios.</h6>
                      <p>
@@ Line 351: / Line 307: @@
                      </p>
                      <ul>
-                    	<li><p>
+                      <li><p>
-                    		A simple, <b>easy-to-understand model</b> that clearly explains the processes of cellular transcription and translation.
+                        A simple, <b>easy-to-understand model</b> that clearly explains the processes of cellular transcription and translation.
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-                    		It is <b>valid for any Printeria construction</b> that has a constitutive expression promoter. The variation between different constructions occurs in the parameters values, not in the model equations!
+                        It is <b>valid for any Printeria construction</b> that has a constitutive expression promoter. The variation between different constructions occurs in the parameters values, not in the model equations!
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-							It has <b>few parameters</b>, with a clear physical meaning, and <b>easily optimizable</b>.
+              It has <b>few parameters</b>, with a clear physical meaning, and <b>easily optimizable</b>.
-						</p></li>
+            </p></li>
-                    	<li><p>
+                      <li><p>
-                    		As a compact model, <b>simulations and optimizations</b> are performed <b>at high speed</b>.
+                        As a compact model, <b>simulations and optimizations</b> are performed <b>at high speed</b>.
-                    	</p></li>
+                      </p></li>
                      </ul>
@@ Line 368: / Line 324: @@
                      <p>
                      The simple model of constitutive expression is a model that characterizes a large number of Printeria Transcriptional Units (TU), specifically, all those constructions whose promoter is constitutive. We know that all these TU follow the <b>same model</b>, but each one has <b>different parameters</b>, and therefore different experimental values of fluorescence and absorbance. Faced with this situation, the Printeria Lab and Modeling teams have designed some experiments, in which we have applied the <a href="#optimization" class="inner-link">multi-objective parameter optimization</a>, and thus check whether the designed constitutive expression model responds to experimental reality.
-                	</p>
+                  </p>
-                	<a class="anchorOffset" id="RBS_exp"></a>
+                  <a class="anchorOffset" id="RBS_exp"></a>
-                	<h7><b>Experiments changing RBS</b></h7>
+                  <h7><b>Experiments changing RBS</b></h7>
-                	<p>
+                  <p>
-                	We have designed <b>two experiments</b> following the same <a href="#https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" class="inner-link">experimental protocol</a>. In them we have assembled different Printeria TU with the same promoters, CDS (<a href="http://parts.igem.org/Part:BBa_K2656013" target="_blank">sfGFP</a> reporter protein) and transcriptional terminator, but with <b>different RBS</b>. After obtaining the results, and following the <a href="#optimization" class="inner-link">optimization protocol</a>, we have obtained the parameters of the model and have validated our model.
+                  We have designed <b>two experiments</b> following the same <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" target="_blank">experimental protocol</a> to assemble different Printeria TUs with the same promoter, CDS (<a href="http://parts.igem.org/Part:BBa_K2656013" target="_blank">sfGFP</a> reporter protein) and transcriptional terminator, but with <b>different RBSs</b>. Once a TU is made, we estimated the model parameters and particularly the RBS of every TU using the <a href="#optimization" class="inner-link"> multiobjective optimization protocol</a>.
-                	</p>
+                  </p>
-                	<a class="anchorOffset" id="RBS_list"></a>
+                  <p><b>Printeria TU</b>:</p>
-                	<p><b>Printeria RBS</b>:</p>
+                  <ul>
-                	<ul>
+                    <li><p>
-                		<li><p>
+                      <b>Strong expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656101" target="_blank" style="padding-right: 0">BBa_K2656101</a>.
-                			<b>Strong expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>.
+                    </p></li>
-                		</p></li>
+                    <li><p>
-                		<li><p>
+                      <b>Medium expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656103" target="_blank" style="padding-right: 0">BBa_K2656103</a>.
-                			<b>Medium expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>.
+                    </p></li>
-                		</p></li>
+                    <li><p>
-                		<li><p>
+                      <b>Weak expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656102" target="_blank" style="padding-right: 0">BBa_K2656102</a>.
-                			<b>Low expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>.
+                    </p></li>
-                		</p></li>
+                    <li><p>
-                		<li><p>
+                      <b>Very weak expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656100" target="_blank" style="padding-right: 0">BBa_K2656100</a>, <a href="http://parts.igem.org/Part:BBa_K2656104" target="_blank" style="padding-right: 0">BBa_K2656104</a>.
-                			<b>Very low expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>, <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>.
+                    </p></li>
-                		</p></li>
+                  </ul>
-                	</ul>
+                  <a class="anchorOffset" id="RBS_list"></a>
-                	<table style="width:100%">
+                  <p><b>Printeria RBS</b>:</p>
-						  <tr>
+                  <ul>
-						    <th><p>Experiment parameters</p></th>
+                    <li><p>
-						    <th><p>Description</p></th>
+                      <b>Strong expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>.
-						  </tr>
+                    </p></li>
-						  <tr>
+                    <li><p>
-						    <td><p>Time</p></td>
+                      <b>Medium expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>.
-						    <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
+                    </p></li>
-						  </tr>
+                    <li><p>
-						  <tr>
+                      <b>Weak expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>.
-						    <td><p>Number of samples</p></td>
+                    </p></li>
-						    <td><p>8 samples for each TU colony</p></td>
+                    <li><p>
-						  </tr>
+                      <b>Very weak expression</b>: <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>, <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>.
-						  <tr>
+                    </p></li>
-						    <td><p>Number of medium samples</p></td>
+                  </ul>
-						    <td><p>8 samples of M9 medium</p></td>
+                  <table style="width:100%">
-						  </tr>
+              <tr>
-						  <tr>
+                <th><p>Experiment parameters</p></th>
-						    <td><p>Temperature</p></td>
+                <th><p>Description</p></th>
-						    <td><p>37 ºC</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Time</p></td>
-						    <td><p>Shake</p></td>
+                <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
-						    <td><p>Double Orbital. Continuously</p></td>
+              </tr>
-						  </tr>
+              <tr>
-							  <tr>
+                <td><p>Number of samples</p></td>
-						    <td><p>Absorbance. Optical Density (OD) measure</p></td>
+                <td><p>8 samples for each TU colony</p></td>
-						    <td><p>Wavelenght at 600 nm emission</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Number of medium samples</p></td>
-						    <td><p>Excitacion wavelength</p></td>
+                <td><p>8 samples of M9 medium</p></td>
-						    <td><p>Wavelenght at 485 nm</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Temperature</p></td>
-						    <td><p>Emission wavelength</p></td>
+                <td><p>37 ºC</p></td>
-						    <td><p>Wavelenght at  528 nm</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Shake</p></td>
-						    <td><p>Gain (G)</p></td>
+                <td><p>Double Orbital. Continuously</p></td>
-						    <td><p>60</p></td>
+              </tr>
-						  </tr>
+                <tr>
-					</table>
+                <td><p>Absorbance. Optical Density (OD) measure</p></td>
+                <td><p>Wavelenght at 600 nm emission</p></td>
+              </tr>
+              <tr>
+                <td><p>Excitacion wavelength</p></td>
+                <td><p>Wavelenght at 485 nm</p></td>
+              </tr>
+              <tr>
+                <td><p>Emission wavelength</p></td>
+                <td><p>Wavelenght at  528 nm</p></td>
+              </tr>
+              <tr>
+                <td><p>Gain (G)</p></td>
+                <td><p>60</p></td>
+              </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Biotek Cytation 3 experimental parameters.</h6>
-					<table style="width:100%">
+          <table style="width:100%">
-						  <tr>
+              <tr>
-						    <th><p>Optimization specifications</p></th>
+                <th><p>Optimization specifications</p></th>
-						    <th><p>Description</p></th>
+                <th><p>Description</p></th>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Parameters</p></td>
+                <td><p>Parameters</p></td>
-						    <td>
+                <td>
-						    	<p>Constitutive transcription rate C<sub>R</sub>: fixed</p>
+                  <p>Constitutive transcription rate C<sub>R</sub>: fixed</p>
-						    	<p><b>Translation rate p: to optimize</b></p>
+                  <p><b>Translation rate p: to optimize</b></p>
-						    	<p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
+                  <p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
-						    	<p>mRNA degradation rate d<sub>m</sub>: fixed</p>
+                  <p>mRNA degradation rate d<sub>m</sub>: fixed</p>
-						    	<p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
+                  <p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
-						    	<p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
+                  <p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
-						    </td>
+                </td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Objetives to optimize</p></td>
+                <td><p>Objetives to optimize</p></td>
-						    <td>
+                <td>
-						    	<p>For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In each experiment we have measured 3 TU, so we are optimizing <b>6 objectives per experiment</b></p>
+                  <p>For each TU, we set 2 objetives: FOD (Fluorescence per cell) and OD (Absorbance). In each experiment we measured 3 TU, so we are optimizing <b>6 objectives per experiment</b></p>
-						    </td>
+                </td>
-						  <tr>
+              <tr>
-						    <td><p>Parameter ranges</p></td>
+                <td><p>Parameter ranges</p></td>
-						    <td>
+                <td>
-						    	<p>Translation rate p: [0.001 - 6] min<sup>-1</sup> </p>
+                  <p>Translation rate p: [0.001 - 6] min<sup>-1</sup> </p>
-						    	<p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.0087] min<sup>-1</sup> </p>
+                  <p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.0087] min<sup>-1</sup> </p>
-						    	<p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
+                  <p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
-						    </td>
+                </td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>MATLAB files</p></td>
+                <td><p>MATLAB files</p></td>
-						    <td>
+                <td>
-						    	<p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
+                  <p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
-						    	<ul>
+                  <ul>
-						    		<li><p>
+                    <li><p>
-						    			Experiment 1: <a href="https://static.igem.org/mediawiki/2018/c/c9/T--Valencia_UPV--spMODEparam_exp1sfGFPUPV2018.txt" target="_blank">spMODEparam_exp1sfGFP.m</a>
+                      Experiment 1: <a href="https://static.igem.org/mediawiki/2018/c/c9/T--Valencia_UPV--spMODEparam_exp1sfGFPUPV2018.txt" target="_blank">spMODEparam_exp1sfGFP.m</a>
-						    		</p></li>
+                    </p></li>
-						    		<li><p>
+                    <li><p>
-						    			Experiment 2: <a href="https://static.igem.org/mediawiki/2018/0/0d/T--Valencia_UPV--spMODEparam_exp2sfGFPUPV2018.txt" target="_blank">spMODEparam_exp2sfGFP.m</a>
+                      Experiment 2: <a href="https://static.igem.org/mediawiki/2018/0/0d/T--Valencia_UPV--spMODEparam_exp2sfGFPUPV2018.txt" target="_blank">spMODEparam_exp2sfGFP.m</a>
-						    		</p></li>
+                    </p></li>
-						    	</ul>
+                  </ul>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt">SphPruning.m</a> file).</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt" target="_blank"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt" target="_blank">SphPruning.m</a> file).</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/9/95/T--Valencia_UPV--CostFunction_RBS_RMS_2nUPV2018.txt" target="_blank"><b>CostFunction_RBS_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/9/95/T--Valencia_UPV--CostFunction_RBS_RMS_2nUPV2018.txt" target="_blank"><b>CostFunction_RBS_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/3/3f/T--Valencia_UPV--execute_RBS_2nUPV2018.txt" target="_blank"><b>execute_RBS_2n.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/3/3f/T--Valencia_UPV--execute_RBS_2nUPV2018.txt" target="_blank"><b>execute_RBS_2n.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
-						    </td>
+                </td>
-						  </tr>
+              </tr>
-					</table>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Optimization specifications for the experiment.</h6>
-					<a href="https://static.igem.org/mediawiki/2018/b/b1/T--Valencia_UPV--optimization_exp1_RBS_graphUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/b/b1/T--Valencia_UPV--optimization_exp1_RBS_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/b/b1/T--Valencia_UPV--optimization_exp1_RBS_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/b/b1/T--Valencia_UPV--optimization_exp1_RBS_graphUPV2018.png" />
-					</a>
+          </a>
-					<h6 style="text-align: left; padding-left: 5em;">Experiment 1 changing RBS. Experimental and optimized simulated model data of strong, medium and low protein expression RBS</h6>
+          <h6 style="text-align: left; padding-left: 5em;">Experiment 1 changing RBS. Experimental and optimized simulated model data of strong, medium and weak protein expression RBS</h6>
-					<a href="https://static.igem.org/mediawiki/2018/7/75/T--Valencia_UPV--optimization_exp2sfGFP_all_graphUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/7/75/T--Valencia_UPV--optimization_exp2sfGFP_all_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/7/75/T--Valencia_UPV--optimization_exp2sfGFP_all_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/7/75/T--Valencia_UPV--optimization_exp2sfGFP_all_graphUPV2018.png" />
-					</a>
+          </a>
-					<h6 style="text-align: left; padding-left: 5em;">Experiment 2 changing RBS. Experimental and optimized simulated model data of strong and very low protein expression RBS</h6>
+          <h6 style="text-align: left; padding-left: 5em;">Experiment 2 changing RBS. Experimental and optimized simulated model data of strong and very weak protein expression RBS</h6>
-					<a href="https://static.igem.org/mediawiki/2018/4/49/T--Valencia_UPV--optimization_exp2_RBS_2obj_graphUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/4/49/T--Valencia_UPV--optimization_exp2_RBS_2obj_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/4/49/T--Valencia_UPV--optimization_exp2_RBS_2obj_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/4/49/T--Valencia_UPV--optimization_exp2_RBS_2obj_graphUPV2018.png" />
-					</a>
+          </a>
-					<h6 style="text-align: left; padding-left: 5em;">Experiment 2 changing RBS. Experimental and optimized simulated model data of very low protein expression RBS</h6>
+          <h6 style="text-align: left; padding-left: 5em;">Experiment 2 changing RBS. Experimental and optimized simulated model data of very weak protein expression RBS</h6>
-					<p>
+          <p>
-					The results of the graphs have been obtained after an optimization and decision-making process, in which the optimal parameters have been selected and the constituent model for each objective has been simulated and compared with the experimental data. The optimized parameters are summarized in the following table.
+          The results above were obtained after an optimization and decision-making process,  where one set of the model parameters were selected to simulate the ODE model of every TU. These simulations were compared with the experimental data showing good agreement. The optimized set of model parameters are summarized in the following table.
-					</p>
+          </p>
-					<table style="width:100%">
+          <table style="width:100%">
-						  <tr>
+              <tr>
-						    <th><p>Optimized parameters</p></th>
+                <th><p>Optimized parameters</p></th>
-						    <th><p>Values</p></th>
+                <th><p>Values</p></th>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						  	<td><p>Translation rate <b>p</b></p></td>
+                <td><p>Translation rate <b>p</b></p></td>
-						  	<td>
+                <td>
-						  		<p><b>Experiment 1</b>:</p>
+                  <p><b>Experiment 1</b>:</p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: p = 0.2059 min<sup>-1</sup>
+                      For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: p = 0.2059 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For medium RBS <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>: p = 0.082 min<sup>-1</sup>
+                      For medium RBS <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>: p = 0.082 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For low RBS <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>: p = 0.01 min<sup>-1</sup>
+                      For weak RBS <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>: p = 0.01 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  		<p><b>Experiment 2</b>:</p>
+                  <p><b>Experiment 2</b>:</p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: p = 0.9256 min<sup>-1</sup>
+                      For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: p = 0.9256 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For very low RBS <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>: p = 0.04089 min<sup>-1</sup>
+                      For very weak RBS <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>: p = 0.04089 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For very low RBS <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>: p = 0.02889 min<sup>-1</sup>
+                      For very weak RBS <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>: p = 0.02889 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  	</td>
+                </td>
-						  </tr>
+              </tr>
-						  <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
+              <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
-						  	<td>
+                <td>
-						  		<p><b>Experiment 1</b>: d<sub>p</sub> = 0.0058 min<sup>-1</sup></p>
+                  <p><b>Experiment 1</b>: d<sub>p</sub> = 0.0058 min<sup>-1</sup></p>
-						  		<p><b>Experiment 2</b>: d<sub>p</sub> = 0.00818 min<sup>-1</sup></p>
+                  <p><b>Experiment 2</b>: d<sub>p</sub> = 0.00818 min<sup>-1</sup></p>
-						  	</td>
+                </td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						  	<td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
+                <td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
-						  	<td>
+                <td>
-						  		<p><b>Experiment 1</b>:</p>
+                  <p><b>Experiment 1</b>:</p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: <meta charset="utf-8">&mu; = 0.01492 min<sup>-1</sup>
+                      For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: <meta charset="utf-8">&mu; = 0.01492 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For medium RBS <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>: <meta charset="utf-8">&mu; = 0.01631 min<sup>-1</sup>
+                      For medium RBS <a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a>: <meta charset="utf-8">&mu; = 0.01631 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For low RBS <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>: <meta charset="utf-8">&mu; = 0.01641 min<sup>-1</sup>
+                      For weak RBS <a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a>: <meta charset="utf-8">&mu; = 0.01641 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  		<p><b>Experiment 2</b>:</p>
+                  <p><b>Experiment 2</b>:</p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: <meta charset="utf-8">&mu; = 0.01197 min<sup>-1</sup>
+                      For strong RBS <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a>: <meta charset="utf-8">&mu; = 0.01197 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For very low RBS <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>: <meta charset="utf-8">&mu; = 0.01288 min<sup>-1</sup>
+                      For very weak RBS <a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a>: <meta charset="utf-8">&mu; = 0.01288 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For very low RBS <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>: <meta charset="utf-8">&mu; = 0.0118 min<sup>-1</sup>
+                      For very weak RBS <a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a>: <meta charset="utf-8">&mu; = 0.0118 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  	</td>
+                </td>
-					</table>
+          </table>
-					<p>
+          <h6 style="text-align: left; padding-left: 5em;">List of optimized parameters for RBS experiment.</h6>
-					In addition to simulating the optimized models, the Printeria Modeling team has also calculated the relative force between the different RBS, taking <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a> strong RBS as a reference. The relative force has been defined as the quotient between the values of the protein in equilibrium of the results of the simulation of one RBS and another reference RBS. Likewise, a ratio between <i>p</i> parameters of the different <a href="#RBS_list" class="inner-link">RBS parts</a> and <i>p</i> parameter of the reference RBS has been calculated. The characterization of the RBS parts by their relative strength is shown below.
+          <p>
+          In addition, the Printeria Modeling team has also calculated the relative strength between the different RBS, taking <a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a> strong RBS as a reference. The relative strength is the quotient between the values of the protein at the equilibrium point and the reference. The characterization of the RBS parts by their relative strength is shown below.
+          </p>
-					<a href="https://static.igem.org/mediawiki/2018/d/d7/T--Valencia_UPV--rel_force_eqUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/d/d9/T--Valencia_UPV--rel_strength_eqUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/d/d7/T--Valencia_UPV--rel_force_eqUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/d/d9/T--Valencia_UPV--rel_strength_eqUPV2018.png" />
-					</a>
+          </a>
-					</p>
+          <table style="width:100%">
-					<table style="width:100%">
+              <tr>
-						  <tr>
+                <th><p>Original BioBrick RBS part</p></th>
-						  	<th><p>Original BioBrick RBS part</p></th>
+                <th><p>Printeria RBS part</p></th>
-						    <th><p>Printeria RBS part</p></th>
+                <th><p>Relative strength</p></th>
-						    <th><p>Relative strength</p></th>
+                <th><p>p parameter ratio (p<sub>RBS</sub>/p<sub>ref</sub>)</p></th>
-						    <th><p>p parameter ratio (p<sub>RBS</sub>/p<sub>ref</sub>)</p></th>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_B0030" target="_blank" style="padding-right: 0">BBa_B0030</a> (<i>Reference part</i>)</p></td>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_B0030" target="_blank" style="padding-right: 0">BBa_B0030</a> (<i>Reference</i>)</p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a> (<i>Reference part</i>)</p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656009" target="_blank" style="padding-right: 0">BBa_K2656009</a> (<i>Reference</i>)</p></td>
+                <td><p>1</p></td>
-						    <td><p>1</p></td>
+                <td><p>1</p></td>
-						    <td><p>1</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_B0034" target="_blank" style="padding-right: 0">BBa_B0034</a></p></td>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_B0034" target="_blank" style="padding-right: 0">BBa_B0034</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656011" target="_blank" style="padding-right: 0">BBa_K2656011</a></p></td>
+                <td><p>0.371</p></td>
-						    <td><p>0.371</p></td>
+                <td><p>0.398</p></td>
-						    <td><p>0.398</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_B0032" target="_blank" style="padding-right: 0">BBa_B0032</a></p></td>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_B0032" target="_blank" style="padding-right: 0">BBa_B0032</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656010" target="_blank" style="padding-right: 0">BBa_K2656010</a></p></td>
+                <td><p>0.045</p></td>
-						    <td><p>0.045</p></td>
+                <td><p>0.048</p></td>
-						    <td><p>0.048</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_J61100" target="_blank" style="padding-right: 0">BBa_J61100</a></p></td>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_J61100" target="_blank" style="padding-right: 0">BBa_J61100</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656008" target="_blank" style="padding-right: 0">BBa_K2656008</a></p></td>
+                <td><p>0.042</p></td>
-						    <td><p>0.042</p></td>
+                <td><p>0.044</p></td>
-						    <td><p>0.044</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_J61101" target="_blank" style="padding-right: 0">BBa_J61101</a></p></td>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_J61101" target="_blank" style="padding-right: 0">BBa_J61101</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656012" target="_blank" style="padding-right: 0">BBa_K2656012</a></p></td>
+                <td><p>0.031</p></td>
-						    <td><p>0.031</p></td>
+                <td><p>0.031</p></td>
-						    <td><p>0.031</p></td>
+              </tr>
-						  </tr>
+          </table>
-					</table>
+          <h6 style="text-align: left; padding-left: 5em;">Relative strength between different RBS parts.</h6>
-					<a class="anchorOffset" id="prom_exp"></a>
+          <a class="anchorOffset" id="prom_exp"></a>
-                	<h7><b>Experiments changing promoters</b></h7>
+                  <h7><b>Experiments changing promoters</b></h7>
-                	<p>
+                  <p>
-                	We have designed <b>two experiments</b> following the same <a href="#https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" class="inner-link">experimental protocol</a>. In them we have assembled different Printeria TU with the same RBS, CDS (<a href="http://parts.igem.org/Part:BBa_K2656022" target="_blank">GFP</a> reporter protein) and transcriptional terminator, and with <b>different promoters</b>. After obtaining the results, and following the <a href="#optimization" class="inner-link">optimization protocol</a>, we have obtained the parameters of the model and have validated our model.
+                  We have designed <b>two experiments</b> following the same <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" target="_blank">experimental protocol</a> to assemble different Printeria TUs with the same RBS, CDS (<a href="http://parts.igem.org/Part:BBa_K2656022" target="_blank">GFP</a> reporter protein) and transcriptional terminator, but with <b>different promoters</b>. Then, following the <a href="#optimization" class="inner-link">optimization protocol</a> we have obtained the model parameters and particularly the promoter values.
-                	</p>
+                  </p>
-                	<a class="anchorOffset" id="promoter_list"></a>
+                  <p><b>Printeria TU</b>:</p>
-                	<p><b>Printeria promoters</b>:</p>
+                  <ul>
-                	<ul>
+                    <li><p>
-                		<li><p>
+                      <b>Strong promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656106" target="_blank" style="padding-right: 0">BBa_K2656106</a>
-                			<b>Strong promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>
+                    </p></li>
-                		</p></li>
+                    <li><p>
-                		<li><p>
+                      <b>Medium promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656107" target="_blank" style="padding-right: 0">BBa_K2656107</a>
-                			<b>Medium promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>
+                    </p></li>
-                		</p></li>
+                    <li><p>
-                		<li><p>
+                      <b>Weak promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656105" target="_blank" style="padding-right: 0">BBa_K2656105</a>
-                			<b>Low promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>
+                    </p></li>
-                		</p></li>
+                  </ul>
-                	</ul>
+                  <a class="anchorOffset" id="promoter_list"></a>
-                	<table style="width:100%">
+                  <p><b>Printeria promoters</b>:</p>
-						  <tr>
+                  <ul>
-						    <th><p>Experiment parameters</p></th>
+                    <li><p>
-						    <th><p>Description</p></th>
+                      <b>Strong promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>
-						  </tr>
+                    </p></li>
-						  <tr>
+                    <li><p>
-						    <td><p>Time</p></td>
+                      <b>Medium promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>
-						    <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
+                    </p></li>
-						  </tr>
+                    <li><p>
-						  <tr>
+                      <b>Weak promoters</b>: <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>
-						    <td><p>Number of samples</p></td>
+                    </p></li>
-						    <td><p>8 samples for each TU colony</p></td>
+                  </ul>
-						  </tr>
+                  <table style="width:100%">
-						  <tr>
+              <tr>
-						    <td><p>Number of medium samples</p></td>
+                <th><p>Experiment parameters</p></th>
-						    <td><p>8 samples of M9 medium</p></td>
+                <th><p>Description</p></th>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Temperature</p></td>
+                <td><p>Time</p></td>
-						    <td><p>37 ºC</p></td>
+                <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Shake</p></td>
+                <td><p>Number of samples</p></td>
-						    <td><p>Double Orbital. Continuously</p></td>
+                <td><p>8 samples for each TU colony</p></td>
-						  </tr>
+              </tr>
-							  <tr>
+              <tr>
-						    <td><p>Absorbance. Optical Density (OD) measure</p></td>
+                <td><p>Number of medium samples</p></td>
-						    <td><p>Wavelenght at 600 nm emission</p></td>
+                <td><p>8 samples of M9 medium</p></td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Excitacion wavelength</p></td>
+                <td><p>Temperature</p></td>
-						    <td><p>Wavelenght at 485 nm</p></td>
+                <td><p>37 ºC</p></td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>Emission wavelength</p></td>
+                <td><p>Shake</p></td>
-						    <td><p>Wavelenght at  528 nm</p></td>
+                <td><p>Double Orbital. Continuously</p></td>
-						  </tr>
+              </tr>
-						  <tr>
+                <tr>
-						    <td><p>Gain (G)</p></td>
+                <td><p>Absorbance. Optical Density (OD) measure</p></td>
-						    <td><p>60</p></td>
+                <td><p>Wavelenght at 600 nm emission</p></td>
-						  </tr>
+              </tr>
-					</table>
+              <tr>
-					<table style="width:100%">
+                <td><p>Excitacion wavelength</p></td>
-						  <tr>
+                <td><p>Wavelenght at 485 nm</p></td>
-						    <th><p>Optimization specifications</p></th>
+              </tr>
-						    <th><p>Description</p></th>
+              <tr>
-						  </tr>
+                <td><p>Emission wavelength</p></td>
-						  <tr>
+                <td><p>Wavelenght at  528 nm</p></td>
-						    <td><p>Parameters</p></td>
+              </tr>
-						    <td>
+              <tr>
-						    	<p><b>Constitutive transcription rate C<sub>R</sub>: to optimize</b></p>
+                <td><p>Gain (G)</p></td>
-						    	<p>Translation rate p: fixed</p>
+                <td><p>60</p></td>
-						    	<p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
+              </tr>
-						    	<p>mRNA degradation rate d<sub>m</sub>: fixed</p>
+          </table>
-						    	<p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
+          <h6 style="text-align: left; padding-left: 5em;">Biotek Cytation 3 experimental parameters.</h6>
-						    	<p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
+          <table style="width:100%">
-						    </td>
+              <tr>
-						  </tr>
+                <th><p>Optimization specifications</p></th>
-						  <tr>
+                <th><p>Description</p></th>
-						    <td><p>Objetives to optimize</p></td>
+              </tr>
-						    <td>
+              <tr>
-						    	<p>For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In each experiment we have measured 3 TU, so we are optimizing <b>6 objectives per experiment</b></p>
+                <td><p>Parameters</p></td>
-						    </td>
+                <td>
-						  <tr>
+                  <p><b>Constitutive transcription rate C<sub>R</sub>: to optimize</b></p>
-						    <td><p>Parameter ranges</p></td>
+                  <p>Translation rate p: fixed</p>
-						    <td>
+                  <p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
-						    	<p>Constitutive transcription rate C<sub>R</sub>: [ - ] min<sup>-1</sup> </p>
+                  <p>mRNA degradation rate d<sub>m</sub>: fixed</p>
-						    	<p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.0087] min<sup>-1</sup> </p>
+                  <p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
-						    	<p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
+                  <p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
-						    </td>
+                </td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						    <td><p>MATLAB files</p></td>
+                <td><p>Objetives to optimize</p></td>
-						    <td>
+                <td>
-						    	<p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
+                  <p>For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In each experiment we have measured 3 TU, so we are optimizing <b>6 objectives per experiment</b></p>
-						    	<ul>
+                </td>
-						    		<li><p>
+              <tr>
-						    			Experiment 1: <a href="" target="_blank">--</a>
+                <td><p>Parameter ranges</p></td>
-						    		</p></li>
+                <td>
-						    	</ul>
+                  <p>Constitutive transcription rate C<sub>R</sub>: 500 x [0.001 - 5] min<sup>-1</sup> </p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt">SphPruning.m</a> file).</p>
+                  <p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.0087] min<sup>-1</sup> </p>
-						    	<p><a href="t" target="_blank"><b>CostFunction_Prom_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
+                  <p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
+                </td>
-						    	<p><a href="" target="_blank"><b>execute.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
+              </tr>
-						    </td>
+              <tr>
-						  </tr>
+                <td><p>MATLAB files</p></td>
-					</table>
+                <td>
+                  <p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
+                  <p>In this experiment, we have used the <a href="https://static.igem.org/mediawiki/2018/0/0c/T--Valencia_UPV--spMODEparam_promUPV2018.txt" target="_blank">spMODEparam_exp6GFP.m</a> MATLAB script.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt" target="_blank"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt" target="_blank">SphPruning.m</a> file).</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/1/14/T--Valencia_UPV--CostFunction_Prom_RMS_2nUPV2018.txt" target="_blank"><b>CostFunction_Prom_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/5/52/T--Valencia_UPV--execute_Prom_2nUPV2018.txt" target="_blank"><b>execute_Prom_2n.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
+                </td>
+              </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Optimization specifications for the experiment.</h6>
+          <a href="https://static.igem.org/mediawiki/2018/d/d9/T--Valencia_UPV--optimization_GFP_promUPV2018.png" data-lightbox="true">
+            <img src="https://static.igem.org/mediawiki/2018/d/d9/T--Valencia_UPV--optimization_GFP_promUPV2018.png" />
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">Experiment 1 changing promoters. Experimental and optimized simulated model data of strong, medium and weak promoters.</h6>
-					<a href="" data-lightbox="true">
+          <p>
-						<img src="" />
+          The results above were obtained after an optimization and decision-making process,  where one set of the model parameters were selected to simulate the ODE model of every TU. These simulations were compared with the experimental data showing good agreement.
-					</a>
+          </p>
+          <table style="width:100%">
+              <tr>
+                <th><p>Optimized parameters</p></th>
+                <th><p>Values</p></th>
+              </tr>
+              <tr>
+                <td><p>Constitutive transcription rate <b>C<sub>R</sub></b></p></td>
+                <td>
+                  <ul>
+                    <li><p>
+                      For strong promoter <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>: C<sub>R</sub> = 539.5 min<sup>-1</sup>
+                    </p></li>
+                    <li><p>
+                      For medium promoter <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>: C<sub>R</sub> = 486.25 min<sup>-1</sup>
+                    </p></li>
+                    <li><p>
+                      For weak promoter <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>: C<sub>R</sub> = 171.15 min<sup>-1</sup>
+                    </p></li>
+                  </ul>
+                </td>
+              </tr>
+              <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
+                <td>
+                  <p>d<sub>p</sub> = 0.008492 min<sup>-1</sup></p>
+                </td>
+              </tr>
+              <tr>
+                <td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
+                <td>
+                  <ul>
+                    <li><p>
+                      For strong promoter <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>: <meta charset="utf-8">&mu; =  0.0072 min<sup>-1</sup>
+                    </p></li>
+                    <li><p>
+                      For medium promoter <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>: <meta charset="utf-8">&mu; =  0.0068 min<sup>-1</sup>
+                    </p></li>
+                    <li><p>
+                      For weak promoter <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>: <meta charset="utf-8">&mu; = 0.011 min<sup>-1</sup>
+                    </p></li>
+                  </ul>
+                </td>
+          </table><p>
+          <h6 style="text-align: left; padding-left: 5em;">List of optimized parameters for promoters experiment.</h6>
-					GRÁFICAS RESULTADOS 2 EXPERIMENTOS PROMOTORES
+          <p>
+          In addition, the Printeria Modeling team has also calculated the relative strength between the different promoters, taking <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a> strong promoter as a reference. The characterization of the promoter parts by their relative strength is shown below.
+          </p>
+          <table style="width:100%">
+              <tr>
+                <th><p>Original BioBrick promoter part</p></th>
+                <th><p>Printeria promoter part</p></th>
+                <th><p>Relative strength</p></th>
+                <th><p>p parameter ratio (p<sub>Prom</sub>/p<sub>ref</sub>)</p></th>
+              </tr>
+              <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_J23102" target="_blank" style="padding-right: 0">BBa_J23102</a> (<i>Reference part</i>)</p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a> (<i>Reference part</i>)</p></td>
+                <td><p>1</p></td>
+                <td><p>1</p></td>
+              </tr>
+              <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_J23101" target="_blank" style="padding-right: 0">BBa_J23101</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a></p></td>
+                <td><p>0.9367</p></td>
+                <td><p>0.9013</p></td>
+              </tr>
+              <tr>
+                <td><p><a href="http://parts.igem.org/Part:BBa_J23106" target="_blank" style="padding-right: 0">BBa_J23106</a></p></td>
+                <td><p><a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a></p></td>
+                <td><p>0.2603</p></td>
+                <td><p>0.3172</p></td>
+              </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Relative strength between different promoter parts.</h6>
+          <a class="anchorOffset" id="tag_exp"></a>
+                  <h7><b>Experiment to compare reporter proteins with and without LVA tag</b></h7>
+                  <p>
+                  In the following experiment we want to compare the <b>degradation rate</b> of different protein reporters in two Printeria TUs with identical promoters, RBS and transcriptional terminators. An <b>LVA degradation tag</b> has been added to one of the protein sequences. This tag causes an increase of protease activity, so it means a <b>faster degradation rate</b> of the reporter protein.  <i>A priori</i>, the degradation rate in the TU with the LVA tag will be higher.
+                  </p>
+                  <p><b>Printeria TU</b>:</p>
+                  <ul>
+                    <li><p>
+                      YFP with LVA tag: <a href="http://parts.igem.org/Part:BBa_K2656111" target="_blank" style="padding-right: 0">BBa_K2656111</a>
+                    </p></li>
+                    <li><p>
+                      YFP without LVA tag: <a href="http://parts.igem.org/Part:BBa_K2656112" target="_blank" style="padding-right: 0">BBa_K2656112</a>
+                    </p></li>
+                  </ul>
+                  <p>
+                  <p><b>Printeria CDS</b>:</p>
+                  <ul>
+                    <li><p>
+                      YFP with LVA tag: <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>
+                    </p></li>
+                    <li><p>
+                      YFP without LVA tag:  <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>
+                    </p></li>
+                  </ul>
+                  <p>
+                  With these experiments, the team aims:
+                  </p>
+                    <ul>
+                      <li><p>
+                        To analyze the effect of the protein degradation rate variation on our <a href="#const_models" class="inner-link">constitutive expression model</a>, and determine if the model fits the experimental results of the reporter proteins with LVA degradation tag.
+                      </p></li>
+                      <li><p>
+                        To characterize the YFP reporter protein with LVA tag as a new iGEM part and as <a href="https://2018.igem.org/Team:Valencia_UPV/Improve" target="_blank">Improve project</a> .
+                      </p></li>
+                    </ul>
                      <p>
-					The results of the graphs have been obtained after an optimization and decision-making process, in which the optimal parameters have been selected and the constituent model for each objective has been simulated and compared with the experimental data. The optimized parameters are summarized in the following table.
+                    The experiments and optimization process performed for each reporter protein are described below. We have followed the <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" target="_blank">experimental protocol</a> and <a href="#optimization" class="inner-link">multi-objective optimization protocol</a>.
-					</p>
+                    </p>
-					<table style="width:100%">
-						  <tr>
-						    <th><p>Optimized parameters</p></th>
-						    <th><p>Values</p></th>
-						  </tr>
-						  <tr>
-						  	<td><p>Constitutive transcription rate <b>C<sub>R</sub></b></p></td>
-						  	<td>
-						  		<ul>
-						  			<li><p>
-						  				For strong promoter <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>: C<sub>R</sub> = - min<sup>-1</sup>
-						  			</p></li>
-						  			<li><p>
-						  				For medium promoter <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>: C<sub>R</sub> = - min<sup>-1</sup>
-						  			</p></li>
-						  			<li><p>
-						  				For low promoter <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>: C<sub>R</sub> = - min<sup>-1</sup>
-						  			</p></li>
-						  		</ul>
-						  	</td>
-						  </tr>
-						  <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
-						  	<td>
-						  		<p><b>Experiment 1</b>: d<sub>p</sub> = - min<sup>-1</sup></p>
-						  	</td>
-						  </tr>
-						  <tr>
-						  	<td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
-						  	<td>
-						  		<ul>
-						  			<li><p>
-						  				For strong promoter <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a>: <meta charset="utf-8">&mu; = - min<sup>-1</sup>
-						  			</p></li>
-						  			<li><p>
-						  				For medium promoter <a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a>: <meta charset="utf-8">&mu; = - min<sup>-1</sup>
-						  			</p></li>
-						  			<li><p>
-						  				For low promoter <a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a>: <meta charset="utf-8">&mu; = - min<sup>-1</sup>
-						  			</p></li>
-						  		</ul>
-						  	</td>
-					</table><p>
-					In addition to simulating the optimized models, the Printeria Modeling team has also calculated the relative force between the different promoters, taking <a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a> promoter as a reference. Likewise, a ratio between <i>C<sub>R</sub></i> parameters of the different <a href="#promoter_list" class="inner-link">promoter parts</a> and <i>C<sub>R</sub></i> parameter of the reference promoter has been calculated. The characterization of the promoter parts by their relative strength is shown below.
-					</p>
-					<table style="width:100%">
-						  <tr>
-						    <th><p>Printeria RBS part</p></th>
-						    <th><p>Relative strength</p></th>
-						    <th><p>p parameter ratio (p<sub>RBS</sub>/p<sub>ref</sub>)</p></th>
-						  </tr>
-						  <tr>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_J23102" target="_blank" style="padding-right: 0">BBa_J23102</a> (<i>Reference</i>)</p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656005" target="_blank" style="padding-right: 0">BBa_K2656005</a> (<i>Reference</i>)</p></td>
-						    <td><p>1</p></td>
-						    <td><p>1</p></td>
-						  </tr>
-						  <tr>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_J23102" target="_blank" style="padding-right: 0">BBa_J23102</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656007" target="_blank" style="padding-right: 0">BBa_K2656007</a></p></td>
-						    <td><p>-</p></td>
-						    <td><p>-</p></td>
-						  </tr>
-						  <tr>
-						  	<td><p><a href="http://parts.igem.org/Part:BBa_J23106" target="_blank" style="padding-right: 0">BBa_J23106</a></p></td>
-						    <td><p><a href="http://parts.igem.org/Part:BBa_K2656004" target="_blank" style="padding-right: 0">BBa_K2656004</a></p></td>
-						    <td><p>-</p></td>
-						    <td><p>-</p></td>
-						  </tr>
-					</table>
-					<a class="anchorOffset" id="tag_exp"></a>
+              <a id="YFP_tag_exp" class="anchorOffset"></a>
-                	<h7><b>Experiment to compare reporter proteins with and without LVA tag</b></h7>
+              <h8><i>YFP with and without LVA tag</i></h8>
-                	<p>
+              <table style="width:100%">
-                	In the following experiment we want to compare the <b>degradation rate</b> of different protein reporters in two Printeria TU with identical promoters, RBS and transcriptional terminators. An <b>LVA degradation tag</b> has been added to one of the protein sequences in one TU. This tag causes an increase in protease activity and, therefore, a <b>faster degradation</b> of the reporter protein in the cell.  <i>A priori</i>, we can deduce that the degradation rate in the TU that presents the degradation tag will be higher.
+              <tr>
-                	</p>
+                <th><p>Experiment parameters</p></th>
-                	<p>
+                <th><p>Description</p></th>
-                	With these experiments, our team aims to meet two objectives:
+              </tr>
-					<ul>
+              <tr>
-						<li><p>
+                <td><p>Time</p></td>
-							To analyze the effect of the protein degradation rate variation on our <a href="#const_models" class="inner-link">constitutive expression model</a>, and determine if the model fits the experimental results of the reporter proteins with LVA degradation tag.
+                <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
-						</p></li>
+              </tr>
-						<li><p>
+              <tr>
-							Characterize the YFP reporter protein with LVA tag as a new iGEM part and as <a href="https://2018.igem.org/Team:Valencia_UPV/Improve" target="_blank">Improve project</a> .
+                <td><p>Number of samples</p></td>
-						</p></li>
+                <td><p>8 samples for each TU colony</p></td>
-					</ul>
+              </tr>
-					<p>
+              <tr>
-					The main parameters of the experiment and optimization for each reporter protein are described below. We have followed the usual <a href="https://2018.igem.org/Team:Valencia_UPV/Experiments#exp_protocol" target="_blank">experimentaL protocol</a> and <a href="#optimization" class="inner-link">multi-objective optimization protocol</a>.
+                <td><p>Number of medium samples</p></td>
-					</p>
+                <td><p>8 samples of M9 medium</p></td>
+              </tr>
+              <tr>
+                <td><p>Temperature</p></td>
+                <td><p>37 ºC</p></td>
+              </tr>
+              <tr>
+                <td><p>Shake</p></td>
+                <td><p>Double Orbital. Continuously</p></td>
+              </tr>
+                <tr>
+                <td><p>Absorbance. Optical Density (OD) measure</p></td>
+                <td><p>Wavelenght at 600 nm emission</p></td>
+              </tr>
+              <tr>
+                <td><p>Excitacion wavelength</p></td>
+                <td><p>Wavelenght at 500 nm</p></td>
+              </tr>
+              <tr>
+                <td><p>Emission wavelength</p></td>
+                <td><p>Wavelenght at 540 nm</p></td>
+              </tr>
+              <tr>
+                <td><p>Gain (G)</p></td>
+                <td><p>60</p></td>
+              </tr>
+          </table>
-                	</p>
+          <h6 style="text-align: left; padding-left: 5em;">Biotek Cytation 3 experimental parameters.</h6>
-                	<a id="YFP_tag_exp" class="anchorOffset"></a>
-                	<h8><i>YFP with and without LVA tag</i></h8>
+          <table style="width:100%">
-                	<table style="width:100%">
+              <tr>
-						  <tr>
+                <th><p>Optimization specifications</p></th>
-						    <th><p>Experiment parameters</p></th>
+                <th><p>Description</p></th>
-						    <th><p>Description</p></th>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Parameters</p></td>
-						    <td><p>Time</p></td>
+                <td>
-						    <td><p>06:00:00 (HH:MM:SS). Measurement interval: 05:00 (MM:SS)</p></td>
+                  <p>Constitutive transcription rate C<sub>R</sub>: fixed</p>
-						  </tr>
+                  <p><b>Translation rate p: to optimize</b></p>
-						  <tr>
+                  <p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
-						    <td><p>Number of samples</p></td>
+                  <p>mRNA degradation rate d<sub>m</sub>: fixed</p>
-						    <td><p>8 samples for each TU colony</p></td>
+                  <p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
-						  </tr>
+                  <p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
-						  <tr>
+                </td>
-						    <td><p>Number of medium samples</p></td>
+              </tr>
-						    <td><p>8 samples of M9 medium</p></td>
+              <tr>
-						  </tr>
+                <td><p>Objetives to optimize</p></td>
-						  <tr>
+                <td>
-						    <td><p>Temperature</p></td>
+                  <p>For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In this experiment we have measured 2 TU, so we are optimizing <b>4 objectives per experiment</b></p>
-						    <td><p>37 ºC</p></td>
+                </td>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>Parameter ranges</p></td>
-						    <td><p>Shake</p></td>
+                <td>
-						    <td><p>Double Orbital. Continuously</p></td>
+                  <p>Constitutive transcription rate C<sub>R</sub>: [0.01 - 2] min<sup>-1</sup> </p>
-						  </tr>
+                  <p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.018] min<sup>-1</sup> </p>
-							  <tr>
+                  <p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
-						    <td><p>Absorbance. Optical Density (OD) measure</p></td>
+                </td>
-						    <td><p>Wavelenght at 600 nm emission</p></td>
+              </tr>
-						  </tr>
+              <tr>
-						  <tr>
+                <td><p>MATLAB files</p></td>
-						    <td><p>Excitacion wavelength</p></td>
+                <td>
-						    <td><p>Wavelenght at 500 nm</p></td>
+                  <p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
-						  </tr>
+                <p>In this experiment, we have used <a href="https://static.igem.org/mediawiki/2018/9/98/T--Valencia_UPV--spMODEparam_exp1YFPUPV2018.txt" target="_blank">spMODEparam_exp1YFP.m</a></p>
-						  <tr>
-						    <td><p>Emission wavelength</p></td>
-						    <td><p>Wavelenght at 540 nm</p></td>
-						  </tr>
-						  <tr>
-						    <td><p>Gain (G)</p></td>
-						    <td><p>60</p></td>
-						  </tr>
-					</table>
-					<table style="width:100%">
-						  <tr>
-						    <th><p>Optimization specifications</p></th>
-						    <th><p>Description</p></th>
-						  </tr>
-						  <tr>
-						    <td><p>Parameters</p></td>
-						    <td>
-						    	<p>Constitutive transcription rate C<sub>R</sub>: fixed</p>
-						    	<p><b>Translation rate p: to optimize</b></p>
-						    	<p><b>PoI degradation rate d<sub>p</sub>: to optimize</b></p>
-						    	<p>mRNA degradation rate d<sub>m</sub>: fixed</p>
-						    	<p><b>Dilution rate <meta charset="utf-8">&mu;: to optimize</b></p>
-						    	<p>Maximum growth capacity K<sub>max</sub>: experimental value</p>
-						    </td>
-						  </tr>
-						  <tr>
-						    <td><p>Objetives to optimize</p></td>
-						    <td>
-						    	<p>For each TU, we set 2 objetives: FOD (Fluorescence) and OD (Absorbance). In this experiment we have measured 2 TU, so we are optimizing <b>4 objectives per experiment</b></p>
-						    </td>
-						  <tr>
-						    <td><p>Parameter ranges</p></td>
-						    <td>
-						    	<p>Constitutive transcription rate C<sub>R</sub>: [0.01 - 2] min<sup>-1</sup> </p>
-						    	<p>PoI degradation rate d<sub>p</sub>: [0.0058 - 0.018] min<sup>-1</sup> </p>
-						    	<p>Dilution rate <meta charset="utf-8">&mu;: [0.0058 - 0.035] min<sup>-1</sup> </p>
-						    </td>
-						  </tr>
-						  <tr>
-						    <td><p>MATLAB files</p></td>
-						    <td>
-						    	<p><b>spMODEparam.m</b>:  it defines the parameters to be optimized, their value ranges, number of objectives, the cost function, the identification and validation experimental data and other spMODE algorithm parameters. When the script is executed, a spMODEDat structure variable is defined. This structure contains all the standardized optimization information that the spMODE algorithm will need for its execution.</p>
-								<p>In this experiment, we have used <a href="https://static.igem.org/mediawiki/2018/9/98/T--Valencia_UPV--spMODEparam_exp1YFPUPV2018.txt" target="_blank">spMODEparam_exp1YFP.m</a></p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt">SphPruning.m</a> file).</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/4/45/T--Valencia_UPV--spMODEUPV2018.txt" target="_blank"><b>spMODE.m</b></a>: it contains the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>, which optimizes parameters for our experimental results (to execute spMODE.m file we need also <a href="https://static.igem.org/mediawiki/2018/9/99/T--Valencia_UPV--SphPruningUPV2018.txt" target="_blank">SphPruning.m</a> file).</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/7/7d/T--Valencia_UPV--CostFunction_improve_RMS_2nUPV2018.txt" target="_blank"><b>CostFunction_improve_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/7/7d/T--Valencia_UPV--CostFunction_improve_RMS_2nUPV2018.txt" target="_blank"><b>CostFunction_improve_RMS_2n.m</b></a>: it simulates the model with different vector parameters, and calculates the Root Mean Square Error with the identification dataset. Then, it returns the error for each objective and parameter vector.</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/e/e4/T--Valencia_UPV--levelDiagramUPV2018.txt" target="_blank"><b>levelDiagram.m</b></a>: plots Pareto front and Pareto set that gives us back the algorithm.</p>
-						    	<p><a href="https://static.igem.org/mediawiki/2018/9/92/T--Valencia_UPV--execute_improve_2nUPV2018.txt" target="_blank"><b>execute_improve_2n.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
+                  <p><a href="https://static.igem.org/mediawiki/2018/9/92/T--Valencia_UPV--execute_improve_2nUPV2018.txt" target="_blank"><b>execute_improve_2n.m</b></a>: this script launches the optimization by executing spMODEparam.m, spMODEm algorithm and levelDiagram.m. Then, allows the user to enter the best parameters, and plots validation experimental data and simulation results in the same graph.</p>
-						    </td>
+                </td>
-						  </tr>
+              </tr>
-					</table>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">Optimization specifications for the experiment.</h6>
-					<p>
+          <p>
-					After executing the experiment and the optimization, and selecting the optimal parameters, we obtain the graphical comparison between the experimental and simulated values.
+          After the multiobjective optimization process, we selected one of the solution for the model parameters and then we compared the model simulations with the experimental data. For both TUs, the simulation results match with the experimental ones.
-					</p>
+          </p>
-					<a href="https://static.igem.org/mediawiki/2018/7/72/T--Valencia_UPV--optimization_exp1_YFP_graphUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/7/72/T--Valencia_UPV--optimization_exp1_YFP_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/7/72/T--Valencia_UPV--optimization_exp1_YFP_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/7/72/T--Valencia_UPV--optimization_exp1_YFP_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6>Experiment YFP vs. YFP tag. Experimental data and optimized model  of the YFP and YFP tag proteins</h6>
-					<table style="width:100%">
+          <table style="width:100%">
-						  <tr>
+              <tr>
-						    <th><p>Optimized parameters</p></th>
+                <th><p>Optimized parameters</p></th>
-						    <th><p>Values</p></th>
+                <th><p>Values</p></th>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						  	<td><p>Translation rate <b>p</b></p></td>
+                <td><p>Translation rate <b>p</b></p></td>
-						  	<td>
+                <td>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: p = 0.4622 min<sup>-1</sup>
+                      For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: p = 0.4622 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For YFP without LVA tag  <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: p = 1.053 min<sup>-1</sup>
+                      For YFP without LVA tag  <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: p = 1.053 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  </tr>
+              </tr>
-						  <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
+              <td><p>PoI degradation rate <b>d<sub>p</sub></b></p></td>
-						  	<td><p>
+                <td><p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: d<sub>p</sub> = 0.01492 min<sup>-1</sup>
+                      For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: d<sub>p</sub> = 0.01492 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For YFP without LVA tag  <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: d<sub>p</sub> = 0.0080 min<sup>-1</sup>
+                      For YFP without LVA tag <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: d<sub>p</sub> = 0.0080 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  	</p></td>
+                </p></td>
-						  </tr>
+              </tr>
-						  <tr>
+              <tr>
-						  	<td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
+                <td><p>Dilution rate <b><meta charset="utf-8">&mu;</b></p></td>
-						  	<td><p>
+                <td><p>
-						  		<ul>
+                  <ul>
-						  			<li><p>
+                    <li><p>
-						  				For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: <meta charset="utf-8">&mu; = 0.01166 min<sup>-1</sup>
+                      For YFP with LVA tag <a href="http://parts.igem.org/Part:BBa_K2656020" target="_blank" style="padding-right: 0">BBa_K2656020</a>: <meta charset="utf-8">&mu; = 0.01166 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  			<li><p>
+                    <li><p>
-						  				For YFP without LVA tag  <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: <meta charset="utf-8">&mu; = 0.01307 min<sup>-1</sup>
+                      For YFP without LVA tag <a href="http://parts.igem.org/Part:BBa_K2656021" target="_blank" style="padding-right: 0">BBa_K2656021</a>: <meta charset="utf-8">&mu; = 0.01307 min<sup>-1</sup>
-						  			</p></li>
+                    </p></li>
-						  		</ul>
+                  </ul>
-						  	</p></td>
+                </p></td>
-					</table>
+          </table>
-					<p>
+          <h6 style="text-align: left; padding-left: 5em;">List of optimized parameters.</h6>
-					At this point, it is easy to see that the degradation rate is significantly higher in the reporter protein data with the degradation LVA tag. If we calculate the ratio between the degradation rate of both YFP reporter proteins, we observe that <b>the value of the protein with LVA tag one is about twice the value of the protein without LVA tag</b>.
+          <p>
-					</p>
+          At this point, it is easy to see that the degradation rate is significantly higher in the reporter protein with the degradation LVA tag than the YFP protein. Computing the ratio of the degradation rates for both YFP proteins, we observe that <b>the value of the protein with the LVA tag is about twice the value of the protein without LVA tag</b>.
+          </p>
-					<a href="https://static.igem.org/mediawiki/2018/7/73/T--Valencia_UPV--dp_ratioUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/7/73/T--Valencia_UPV--dp_ratioUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/7/73/T--Valencia_UPV--dp_ratioUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/7/73/T--Valencia_UPV--dp_ratioUPV2018.png" />
-					</a>
+          </a>
+          <a class="anchorOffset" id="ind_models"></a>
+          <h4>Inducible expression models</h4>
+          <p>
+          Inducible expression models are those where protein expression depends on one or more inducing molecules. They are called <b>activators or repressors</b>. The concentration of these biochemical species determines if the transcription is activated or repressed, respectively.</p>
+          <p>
+          Our Printeria device gives us the possibility to create some inducible genetic constructs:
+          </p>
+          <ul>
+            <li><p>
+              <a href="#pBAD" class="inner-link">P<sub>BAD</sub>/araC inducible model</a>
+            </p></li>
+            <li><p>
+              <a href="#LuxR_LuxI" class="inner-link">AHL-LuxR inducible model</a>
+            </p></li>
+          </ul>
-                    <a class="anchorOffset" id="ind_models"></a>
+          <a class="anchorOffset" id="pBAD"></a>
-                    <h4>Inducible expression models</h4>
+          <h5>P<sub>BAD</sub>/araC inducible model</h5>
+          <p>
-					<p>
+          The inducible promoter P<sub>BAD</sub>/araC [<a href="#references" class="inner-link">5</a>] is a promoter whose expression depends on two inducing complexes: the <b>L-arabinose</b> (activator) and the <b>araC</b> (repressor). The dimeric protein araC binds DNA to compound a DNA loop and thus prevents the binding between DNA and RNA polymerase. However, when two arabinose molecules bind the araC dimer, the DNA loop is broken and the binding between the RNA polymerase and the promoter region is possible.
-					Inducible expression models are those in which the expression of the <b>cell's messenger RNA (mRNA) depends on one or more inducing molecules</b>, which can act as <b>activators or repressors</b>. The concentration of the inducing species determines the level of expression of mRNA and protein in the cell.</p>
+          </p>
-					<p>
+          <p>
-					Our Printeria device gives us the possibility to create some inducible genetic constructs. Of all of them, we have managed to design and experiment with some models...
+          We have proposed an ODE model describing the P<sub>BAD</sub>/araC mechanism. This <b>theoretical model</b> has been included in the <a href="#simtool" class="inner-link">Simulation Tool</a>, so Printeria is able to predict the behavior of the P<sub>BAD</sub>/araC inducible promoter circuits.
-					</p>
+          </p>
-					<ul>
+          <h5><i>Model design</i></h5>
-						<li><p>
+          <p>
-							<a href="#pBAD" class="inner-link">P<sub>BAD</sub>/araC inducible model</a>
+          We propose the following scheme that describe the biochemical reactions of the  P<sub>BAD</sub>/araC system. We have assumed a very high concentration of araC inside the cell because the gene encoding for the araC protein is found in the cell genome of some strains (e.g. in DH5<meta charset="utf-8">&alpha; strains).
-						</p></li>
+          </p>
-						<li><p>
-							<a href="#LuxR_LuxI" class="inner-link">LuxR-LuxI inducible model</a>
-						</p></li>
-						<li><p>
-							<a href="#HSP" class="inner-link">LuxR-LuxI inducible model</a>
-						</p></li>
-					</ul>
-					<a class="anchorOffset" id="pBAD"></a>
+          <a href="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--esq_pbadUPV2018.png" data-lightbox="true">
-                    <h5>P<sub>BAD</sub>/araC inducible model</h5>
+            <img src="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--esq_pbadUPV2018.png" />
-					<p>
+          </a>
-					The inducible promoter P<sub>BAD</sub>/araC [<a href="#references" class="inner-link">5</a>] is a promoter whose expression depends on two inducing molecules: the <b>L-arabinose</b> (activator) and the <b>araC</b> (repressor). The dimeric protein araC binds to the DNA chain forming a DNA loop and thus prevents the binding between DNA and RNA polymerase. However, when two arabinose molecules bind to the araC dimer, the DNA loop is broken and the binding between the RNA polymerase to the promoting region is possible.
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Cell schema.</h6>
-					</p>
-					<p>
-					We have proposed a possible mathematical model describing the P<sub>BAD</sub>/araC mechanism. This <b>theoretical model</b> has been included in the <a href="#simtool" class="inner-link">Simulation Tool</a>, so that with Printeria it is possible to predict the behavior of P<sub>BAD</sub>/araC inducible promoter circuits.
-					</p>
-					<h5><i>Model design</i></h5>
-					<p>
-					After analyzing the biochemical functioning of the  P<sub>BAD</sub>/araC promoter, we propose the following cellular scheme that would describe its behavior. It is worth mentioning that we have assumed a very high concentration of araC in the cell, as we have considered that the gene encoding for the araC protein is found in the cell genome (e.g. in DH5<meta charset="utf-8">&alpha; strains).
-					</p>
-					<a href="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--esq_pbadUPV2018.png" data-lightbox="true">
+          <p>From the cell schema we infer the following biochemical reactions:</p>
-						<img src="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--esq_pbadUPV2018.png" />
-					</a>
-					<p>From the cell schema we can deduce the following biochemical reactions.</p>
+          <a href="https://static.igem.org/mediawiki/2018/d/d8/T--Valencia_UPV--react_pbadUPV2018.png" data-lightbox="true">
+            <img src="https://static.igem.org/mediawiki/2018/d/d8/T--Valencia_UPV--react_pbadUPV2018.png" />
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Biochemical reations.</h6>
-					<a href="https://static.igem.org/mediawiki/2018/d/d8/T--Valencia_UPV--react_pbadUPV2018.png" data-lightbox="true">
+          <table style="width:100%">
-						<img src="https://static.igem.org/mediawiki/2018/d/d8/T--Valencia_UPV--react_pbadUPV2018.png" />
+            <tr>
-					</a>
+              <th><p>Parameter</p></th>
+              <th><p>Description</p></th>
+              <th><p>Units</p></th>
+              <th><p>Value</p></th>
+            </tr>
+             <tr>
+              <td><p>D</p></td>
+              <td><p>Diffusion coefficient</p>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>2 [<a href="#references2" class="inner-link">2</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>V<sub>c</sub></p></td>
+              <td><p>Cell volume(1.1x10<sup>-9</sup> <meta charset="utf-8">&mu;L)/External volume(1x10<sup>-3</sup> <meta charset="utf-8">&mu;L)</p>
+              <td><p>adimensional</sup></p></td>
+              <td><p>1.1x10<sup>-6</sup> [<a href="#references2" class="inner-link">2</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>u</sub></p></td>
+              <td><p>Dissociation rate of (P<sub>BAD</sub>.araC.arabi) complex</p>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>10 [<a href="#references10" class="inner-link">10</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>d</sub></p></td>
+              <td><p>Dissociation constant of (P<sub>BAD</sub>.araC.arabi) complex</p>
+              <td><p>molec<sup>2</sup></p></td>
+              <td><p>100 [<a href="#references2" class="inner-link">2</a>, <a href="#references10" class="inner-link">10</a> ]</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>b</sub></p></td>
+              <td><p>Association rate of (P<sub>BAD</sub>.araC.arabi) complex. k<sub>u</sub>/k<sub>d</sub></p>
+              <td><p>molec<sup>-2</sup>min<sup>-1</sup></p></td>
+              <td><p>0.1 (Estimated)</p></td>
+             </tr>
+             <tr>
+              <td><p>K</p></td>
+              <td><p>Transcription rate is the product of transcription rate per plasmid K<sub>t</sub> and the mean number of plasmids in cell c<sub>n</sub> . In our case, we are using the pMBI replication origin, so c<sub>n</sub> <meta charset="utf-8">&sim; 500, and K = K<sub>t</sub>·c<sub>n</sub>.</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>326 [<a href="#references1" class="inner-link">1</a>, <a href="#references7" class="inner-link">7</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p><meta charset="utf-8">&alpha;</p></td>
+              <td><p>(P<sub>BAD</sub>.araC) basal activity constant</p>
+              <td><p>adimensional</p></td>
+              <td><p>0.01 (Estimated)</p></td>
+             </tr>
+              <td><p>p</p></td>
+              <td><p>mRNA translation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>2.38 [<a href="#references2" class="inner-link">2</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>arab</sub></p></td>
+              <td><p>L-arabinose degradation rate. We assume a very slow degradation.</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p><meta charset="utf-8">&sim;10<sup>-6</sup></p></td>
+             </tr>
+             <tr>
+             <tr>
+              <td><p>d<sub>m</sub></p></td>
+              <td><p>mRNA degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.247 [<a href="#references7" class="inner-link">7</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>p</sub></p></td>
+              <td><p>PoI degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.0063 [<a href="#references5" class="inner-link">5</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p><meta charset="utf-8">&mu;</p></td>
+              <td><p>Dilution rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.017 [<a href="#references5" class="inner-link">5</a>]</p></td>
+             </tr>
+             <tr>
+              <td><p>K<sub>max</sub></p></td>
+              <td><p>Maximum growth capacity</p></td>
+              <td><p>cells</p></td>
+              <td><p>1.6·10<sup>8</sup> [<a href="#references5" class="inner-link">5</a>]</p></td>
+             </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Model parameters.</h6>
+            <p>
+            We apply the <a href="#LMA" class="inner-link">Law of Mass Action kynetics</a> (LMA) to obtain the equivalent ODE model. Considerin the same previous assumptions for the constitutive models, and also the fact the the plasmid copy number c<sub>n</sub> is kept as a constant, we can obtain a <b>reduced oreder model</b>. Thus, we get a model of <b>six differential equations</b> and <b>one algebraic equation</b> as below.
+            </p>
+            <table style="width:100%">
+            <tr>
+              <th><p>Variable</p></th>
+              <th><p>Biochemical species</p></th>
+              <th><p>Units</p></th>
+            </tr>
+             <tr>
+              <td><p>n<sub>1</sub></p></td>
+              <td><p>(P<sub>BAD</sub>.araC.arab) complex</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>2</sub></p></td>
+              <td><p>Extracellular L-arabinose</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>3</sub></p></td>
+              <td><p>Intracellular L-arabinose</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+            </tr>
+             <tr>
+              <td><p>n<sub>4</sub></p></td>
+              <td><p>mRNA</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>5</sub></p></td>
+              <td><p>PoI</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>6</sub></p></td>
+              <td><p>Number of cells</p></td>
+              <td><p>Cells</p></td>
+             </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Biochemical species.</h6>
-					<table style="width:100%">
+          <a href="https://static.igem.org/mediawiki/2018/c/c4/T--Valencia_UPV--pbad_alg_eqUPV2018.png" data-lightbox="true">
-						<tr>
+            <img src="https://static.igem.org/mediawiki/2018/c/c4/T--Valencia_UPV--pbad_alg_eqUPV2018.png" />
-						  <th><p>Parameter</p></th>
+          </a>
-						  <th><p>Description</p></th>
-						  <th><p>Units</p></th>
-						  <th><p>Value</p></th>
-						</tr>
-						 <tr>
-						  <td><p>D</p></td>
-						  <td><p>Diffusion coefficient</p>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>V<sub>c</sub></p></td>
-						  <td><p>Cell volume(<meta charset="utf-8">&mu;L)/External volume(<meta charset="utf-8">&mu;L)</p>
-						  <td><p>adimensional</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>k<sub>u</sub></p></td>
-						  <td><p>Dissociation rate of (P<sub>BAD</sub>.araC.arabi) complex</p>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>k<sub>d</sub></p></td>
-						  <td><p>Dissociation constant of (P<sub>BAD</sub>.araC.arabi) complex</p>
-						  <td><p>molec<sup>2</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>k<sub>b</sub></p></td>
-						  <td><p>Association rate of (P<sub>BAD</sub>.araC.arabi) complex</p>
-						  <td><p>molec<sup>-2</sup>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>K</p></td>
-						  <td><p>Transcription rate is calculated by multiplying the transcription rate per plasmid K<sub>t</sub> by the mean number of plasmids in cell c<sub>n</sub> . In our case, we are using the pMBI replication origin, so c<sub>n</sub> <meta charset="utf-8">&sim; 500, and C<sub>R</sub> = K<sub>R</sub>·c<sub>n</sub>.</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p><meta charset="utf-8">&alpha;</p></td>
-						  <td><p>(P<sub>BAD</sub>.araC) basal activity constant</p>
-						  <td><p>adimensional</p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>p</p></td>
-						  <td><p>Translation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>d<sub>arab</sub></p></td>
-						  <td><p>L-arabinose degradation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>d<sub>m</sub></p></td>
-						  <td><p>mRNA degradation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>d<sub>p</sub></p></td>
-						  <td><p>PoI degradation rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p><meta charset="utf-8">&mu;</p></td>
-						  <td><p>Dilution rate</p></td>
-						  <td><p>min<sup>-1</sup></p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-						 <tr>
-						  <td><p>K<sub>max</sub></p></td>
-						  <td><p>Maximum growth capacity</p></td>
-						  <td><p>cells</p></td>
-						  <td><p><a href="">---</a></p></td>
-						 </tr>
-					</table>
-                    <p>
-                    We apply the <a href="#LMA" class="inner-link">Law of Mass Action kynetics</a> (LMA) to obtain the differential equations. If we consider that the plasmid copy number c<sub>n</sub> is constant, we can <b>reduce the model</b> in a differential equation and add an algebraic equation. Thus, we get a model of <b>six differential equations</b> and <b>one algebraic equation</b>, as shown below.
-                    </p>
-                    <table style="width:100%">
-						<tr>
-						  <th><p>Variable</p></th>
-						  <th><p>Biochemical species</p></th>
-						  <th><p>Units</p></th>
-						</tr>
-						 <tr>
-						  <td><p>n<sub>1</sub></p></td>
-						  <td><p>(P<sub>BAD</sub>.araC.arab) complex</p></td>
-						  <td><p>Molecules</p></td>
-						 </tr>
-						 <tr>
-						  <td><p>n<sub>2</sub></p></td>
-						  <td><p>Extracellular L-arabinose</p></td>
-						  <td><p>Molecules</p></td>
-						 </tr>
-						 <tr>
-						  <td><p>n<sub>3</sub></p></td>
-						  <td><p>Intracellular L-arabinose</p></td>
-						  <td><p>Molecules</p></td>
-						 </tr>
-						</tr>
-						 <tr>
-						  <td><p>n<sub>4</sub></p></td>
-						  <td><p>mRNA</p></td>
-						  <td><p>Molecules</p></td>
-						 </tr>
-						 <tr>
-						  <td><p>n<sub>5</sub></p></td>
-						  <td><p>PoI</p></td>
-						  <td><p>Molecules</p></td>
-						 </tr>
-						 <tr>
-						  <td><p>n<sub>6</sub></p></td>
-						  <td><p>Number of cells</p></td>
-						  <td><p>Cells</p></td>
-						 </tr>
-					</table>
-					<a href="https://static.igem.org/mediawiki/2018/c/c4/T--Valencia_UPV--pbad_alg_eqUPV2018.png" data-lightbox="true">
+          <a href="https://static.igem.org/mediawiki/2018/4/40/T--Valencia_UPV--pbad_eqsUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/c/c4/T--Valencia_UPV--pbad_alg_eqUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/4/40/T--Valencia_UPV--pbad_eqsUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Model equations.</h6>
-					<a href="https://static.igem.org/mediawiki/2018/4/40/T--Valencia_UPV--pbad_eqsUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/4/40/T--Valencia_UPV--pbad_eqsUPV2018.png" />
-					</a>
                      <p>
-                     Having developed the equation model from the cell schema and biochemical reactions, we have programmed two MATLAB files: the <a href="https://static.igem.org/mediawiki/2018/d/d4/T--Valencia_UPV--mi_araC_simplestUPV2018.txt" target="_blank">mi_araC_simplest.m</a> function, which describes the system of differential equations, and the script <a href="https://static.igem.org/mediawiki/2018/b/b6/T--Valencia_UPV--model_ind_araC_simplestUPV2018.txt" target="_blank">model_inducible_simplest.m</a> in which the parameters are defined and the model is solved by the <a href="https://es.mathworks.com/help/matlab/ref/ode23t.html" style="padding-right: 0" target="_blank">ode23t</a> MATLAB function. The result of the simulation of the model is shown below.
+                     Now we have two MATLAB files: the <a href="https://static.igem.org/mediawiki/2018/d/d4/T--Valencia_UPV--mi_araC_simplestUPV2018.txt" target="_blank">mi_araC_simplest.m</a> function, which describes the ODE model, and the script <a href="https://static.igem.org/mediawiki/2018/b/b6/T--Valencia_UPV--model_ind_araC_simplestUPV2018.txt" target="_blank">model_inducible_simplest.m</a> where the parameters are defined. The model was simulated by using the <a href="https://es.mathworks.com/help/matlab/ref/ode23t.html" style="padding-right: 0" target="_blank">ode23t</a> MATLAB function. The simulation results are shown below.
                      </p>
                      <a href="https://static.igem.org/mediawiki/2018/5/5a/T--Valencia_UPV--model_ind_araC_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/5/5a/T--Valencia_UPV--model_ind_araC_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/5/5a/T--Valencia_UPV--model_ind_araC_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model. Model predictions using parameter values from literature.</h6>
-            		<p>
+                <p>
-            		Once the P<sub>BAD</sub>/araC model is developed and coded, we <b>simulate the model by varying the parameters</b> through our MATLAB script <a href="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--analysis_miAraC_simplestUPV2018.txt" target="_blank">analysis_mi_araC_simplest.m</a>. In this case, <b>we have varied the K transcription and p translation rates</b> and we have represented in a 3D graph the values of the PoI in the steady state.
+                Once the P<sub>BAD</sub>/araC model was validated, we <b>simulated the model varying the some of its parameters</b> (MATLAB script <a href="https://static.igem.org/mediawiki/2018/3/3c/T--Valencia_UPV--analysis_miAraC_simplestUPV2018.txt" target="_blank">analysis_mi_araC_simplest.m</a>). In this case, <b>we have modified the K transcription rate and the p translation rate</b>.
-            		</p>
+                </p>
-            		<a href="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--analysis_miAraC_graphUPV2018.png" data-lightbox="true">
+                <a href="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--analysis_miAraC_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--analysis_miAraC_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--analysis_miAraC_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model analysis. The graph represents de PoI stationary value as function of p and K ratios.</h6>
-            		<p>As we can see in the 3D graph, the PoI expression growths exponentially when translation rate p and transcription rate K increase.<p>
+                <p>As we can see in the 3D graph, the protein expression of PoI exponentially increases when the translation rate p and transcription rate K become higher.<p>
-            		<p>
+                <p>
-            		But we can also vary the initial concentration of L-arabinose in P<sub>BAD</sub>/araC model. The set of <b>simulations varying p and arab<sub>0</sub> parameters</b> has been programmed in the <a href="https://static.igem.org/mediawiki/2018/6/65/T--Valencia_UPV--analysis_miAraC_simplest_arabUPV2018.txt" target="_blank">analysis_mi_araC_simplest_arab.m</a> MATLAB script. We have represented our results of the PoI in the steady state in a 3D graph.
+                But we can also change the initial concentration of L-arabinose in the P<sub>BAD</sub>/araC model as shown in the figure below. The <b>simulations for several p and arab<sub>0</sub> parameters</b> were ran using the <a href="https://static.igem.org/mediawiki/2018/6/65/T--Valencia_UPV--analysis_miAraC_simplest_arabUPV2018.txt" target="_blank">analysis_mi_araC_simplest_arab.m</a> MATLAB script.
-            		</p>
+                </p>
-            		<a href="https://static.igem.org/mediawiki/2018/3/32/T--Valencia_UPV--analysis_miAraC_simplest_arab_graphUPV2018.png" data-lightbox="true">
+                <a href="https://static.igem.org/mediawiki/2018/3/32/T--Valencia_UPV--analysis_miAraC_simplest_arab_graphUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/3/32/T--Valencia_UPV--analysis_miAraC_simplest_arab_graphUPV2018.png" />
+            <img src="https://static.igem.org/mediawiki/2018/3/32/T--Valencia_UPV--analysis_miAraC_simplest_arab_graphUPV2018.png" />
-					</a>
+          </a>
+          <h6 style="text-align: left; padding-left: 5em;">P<sub>BAD</sub>/araC inducible model analysis. The graph represents de PoI stationary value as function of p ratio and L-arabinose concentration (arab<sub>0</sub>).</h6>
+            <a class="anchorOffset" id="LuxR_LuxI"></a>
+            <h5>AHL-LuxR inducible model</h5>
+            <p>
+            The AHL-LuxR genetic circuit [<a href="#references2" class="inner-link">2</a>] is a more complex genetic circuit than the models presented so far. It couples <b>two functional subsystems</b>: <b>i) quorum sensing interconnecting cell population</b> with the external inducer AHL, and <b>ii) an intracellular loop to regulate expression of the protein of interest</b>.
+            </p>
+            <p>
+            The first subsystem implements a cell-to-cell communication mechanism via quorum sensing. It is based on the exchange of the small signaling autoinducer molecule <b>N-acyl-L-homoserine lactone (AHL)</b> to induce population cell consensus. <b>AHL molecules passively diffuses across the cellular membrane</b> from inside the cell to the external environment, and viceversa, following <b>Fick’s Law</b>.
+            </p>
+            <p>
+            The second subsystem introduces an intracellular loop to control expression of the protein of interest, in this case GFP. First, <b>LuxR protein is expressed by luxR under the constitutive promoter Pc</b>. Then, LuxR and AHL bind forming the heterodimer (LuxR.AHL), which subsequently dimerizes as the heterotetramer transcription factor <b>(LuxR.AHL)<sub>2</sub></b>. The <b>dimer represses protein expression</b> when it is attached to the <b>promoter Plux</b>.
+            </p>
-					<a class="anchorOffset" id="LuxR_LuxI"></a>
+            <h5><i>Model design</i></h5>
-                    <h5>LuxR-LuxI inducible model</h5>
+          <p>
+          We propose the following biochemical reactions based on the Boada et al.(2017) model [<a href="#references2" class="inner-link">2</a>].
+          </p>
-                    <a class="anchorOffset" id="HSP"></a>
+            <a href="https://static.igem.org/mediawiki/2018/3/3d/T--Valencia_UPV--luxR_luxI_schemaUPV2018.png" data-lightbox="true">
-                    <h5>Heat Shock Promoter inducible model</h5>
+            <img src="https://static.igem.org/mediawiki/2018/3/3d/T--Valencia_UPV--luxR_luxI_schemaUPV2018.png" />
+            </a>
+            <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Cell schema.</h6>
+            <p>
+            From the schema, we can obtain the following biochemical reactions:
+            </p>
-                    <a class="anchorOffset" id="optimization"></a>
+            <a href="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--luxR_luxI_reactionsUPV2018.png" data-lightbox="true">
-                    <h4>Multi-objective parameter optimization</h4>
+            <img src="https://static.igem.org/mediawiki/2018/5/57/T--Valencia_UPV--luxR_luxI_reactionsUPV2018.png" />
-                    <p>
+            </a>
-                    <b>To what extent is our model valid? What values should the parameters take? To what extent do the theoretical results resemble the experimental ones? Is our model able to explain the behaviour of cells in reality?</b>
+            <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Biochemical reactions.</h6>
-                    </p>
-                    <p>
+            <table style="width:100%">
-                    One of the most important phases in the field of Printeria Modeling has been the <b>validation of theoretical models</b> with experimental data. In the Printeria team we wanted to confirm that the models designed are consistent with our experiments. However, we know that the <b>parameters will not take a fixed value</b>, but vary depending on the genetic construction with which we experiment. With this idea in mind, the need to apply an optimization process arises.
-                    </p>
+            <tr>
-                    <p>
+              <th><p>Parameter</p></th>
-                    The process of <b>multiobjective parameter optimization</b> [<a href="#references" class="inner-link">3</a>] consists in minimize two or more design objectives that have a trade-off between them as function of some decision variables. In our case, <b>these objectives are estimation errors between experimental data and model predictions</b>, and the <b>decission variables are some of our model parameters</b>. From a dataset, and applying a mathematical algorithm, we can find the <b>optimal solutions, also known as Pareto-optimal</b>. These optimal solutions are such that there are no more solutions that do not improve one objective without worsening the rest.
+              <th><p>Description</p></th>
-                    </p>
+              <th><p>Units</p></th>
-                    <p>
+              <th><p>Value</p></th>
-                    As this is a multi-objective optimization, there is usually no single optimal solution, but rather a set of them which form the <a href="https://static.igem.org/mediawiki/2018/a/ad/T--Valencia_UPV--pfrontUPV2018.png" target="_blank"><b>Pareto front</b></a>. For each of these solutions, we find a set of decision variables associated: the <a href="https://static.igem.org/mediawiki/2018/c/ce/T--Valencia_UPV--psetUPV2018.png" target="_blank"><b>Pareto set</b></a>. In our case, the Pareto front solutions represent the RMS error between experimental data and simulations, and the Pareto set is the set of parameters that give rise to these solutions.
+            </tr>
-                    </p>
+             <tr>
-                    <p>
+              <td><p>C<sub>R</sub></p></td>
-                    From the Printeria Modeling team we have established a protocol that allows us to obtain the optimal solutions of the model parameters for any experiment:
+              <td><p>Constitutive transcription rate is the transcription rate K<sub>R</sub> times the mean plasmid copy number in cell c<sub>n</sub>. In our case, we are using the pACYC replication origin, so c<sub>n</sub> <meta charset="utf-8">&sim; 10, and C<sub>R</sub> = K<sub>R</sub>·c<sub>n</sub></p></td>
-                    </p>
+              <td><p>molecules.min<sup>-1</sup></p></td>
-                    <ol>
+              <td><p>7.9</p></td>
-                    	<li><p>
+             </tr>
-                    		We define the objectives to be optimized. These will be the values of Fluorescence F/Unit of Absorbance OD or FOD, and the cellular growth (OD) of a Transcriptional Unit (TU). Therefore, if we have different <i>n</i> TU in an experiment, we will optimize <i>2n</i> objectives.
+             <tr>
-                    	</p></li>
+              <td><p>k<sub>e<sub>G</sub></sub></p></td>
-                    	<li><p>
+              <td><p>gGFP transcription rate</p></td>
-                    		We choose the parameters to optimize and establish the range of values they can take.
+              <td><p>molecules.min<sup>-1</sup></p></td>
-                    	</p></li>
+              <td><p>17.5</p></td>
-                    	<li><p>
+             </tr>
-                    		We select the identification and validation data. The identification data are those used in the optimization process. The validation data are used to compare the experiment with the simulated theoretical model and the optimized parameters.
+             <tr>
-                    	</p></li>
+              <td><p><meta charset="utf-8">&alpha;</p></td>
-                    	<li><p>
+              <td><p>P<sub>luxR</sub> promoter basal activity</p>
-                    		We define the cost function, which specifies the error function to be minimized, simulates the model with different parameter values, and calculates the error between the simulation data and the experimental identification data.
+              <td><p>adimensional</p></td>
-                    	</p></li>
+              <td><p>0.1 (Estimated)</p></td>
-                    	<li><p>
+             </tr>
-                    		The mathematical optimization algorithm is executed. In our case we use the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>. This algorithm uses the cost function to test different parameter values and thus search for optimal parameter values.
+             <tr>
-                    	</p></li>
+              <td><p>p<sub>R</sub></p></td>
-                    	<li><p>
+              <td><p>m<sub>R</sub> translation rate</p></td>
-                    		The Pareto set and Pareto front diagrams and the different solutions of our optimized parameters for the different objectives are obtained.
+              <td><p>min<sup>-1</sup></p></td>
-                    	</p></li>
+              <td><p>10</p></td>
-                    	<li><p>
+             </tr>
-							Decision Making is carried out by the designer. The optimal parameters are chosen for our <i>2n</i> objectives.
+             <tr>
-                    	</p></li>
+              <td><p>p<sub>G</sub></p></td>
-                    	<li><p>
+              <td><p>m<sub>GFP</sub> translation rate</p></td>
-                    		The model is simulated with the optimized parameters and compared with the validation data.
+              <td><p>min<sup>-1</sup></p></td>
-                    	</p></li>
+              <td><p>3.09</p></td>
-                    </ol>
+             </tr>
-                    <p>
+             <tr>
-                    Following this protocol, and particularizing it for each experiment, we have been able to determine the validity of our models and obtain the best parameters for our experiments.
+              <td><p>k<sub>A</sub></td>
-                    </p>
+              <td><p>Synthesis rate of AHL by LuxI</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.04</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>-1</sub></p></td>
+              <td><p>Dissociation rate of (R·A)</p>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>10</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>-2</sub></p></td>
+              <td><p>Dissociation rate of (R·A)<sub>2</sub></p>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>1</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>d1</sub></p></td>
+              <td><p>Dissociation constant of (R·A)</p>
+              <td><p>molecules</p></td>
+              <td><p>100</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>d2</sub></p></td>
+              <td><p>Dissociation constant of (R·A)<sub>2</sub></p>
+              <td><p>molecules</p></td>
+              <td><p>20</p></td>
+             </tr>
+             <tr>
+              <td><p>k<sub>dlux</sub></p></td>
+              <td><p>Dissociation constant of (R·A)<sub>2</sub> to the P<sub>luxR</sub> promoter</p>
+              <td><p>molecules</p></td>
+              <td><p>10</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>G</sub></p></td>
+              <td><p>GFP degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.027</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>R</sub></p></td>
+              <td><p>R degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.2</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>A</sub></p></td>
+              <td><p>A degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.057</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>A<sub>e</sub></sub></p></td>
+              <td><p>A degradation rate in culture medium</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.057</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>RA</sub></p></td>
+              <td><p>(R·A) degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.156</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>RA<sub>2</sub></sub></p></td>
+              <td><p>(R·A)<sub>2</sub> degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.017</p></td>
+             </tr>
+             <tr>
+              <td><p>d<sub>m<sub>R</sub></sub></p></td>
+              <td><p>m<sub>R</sub> degradation rate</p></td>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>0.247</p></td>
+             </tr>
+             <tr>
+              <td><p>D</p></td>
+              <td><p>Diffusion coefficient of AHL through the cell membrane</p>
+              <td><p>min<sup>-1</sup></p></td>
+              <td><p>2</p></td>
+             </tr>
+             <tr>
+              <td><p>V<sub>c</sub></p></td>
+              <td><p>Cell volume(1.1x10<sup>-9</sup> <meta charset="utf-8">&mu;L)/External volume(1x10<sup>-3</sup> <meta charset="utf-8">&mu;L)</p>
+              <td><p>adimensional</sup></p></td>
+              <td><p>1.1x10<sup>-6</sup></p></td>
+             </tr>
+             <tr>
+              <td><p>N</p></td>
+              <td><p>Number of cells</p>
+              <td><p>cells</p></td>
+              <td><p>240</p></td>
+             </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Model parameters.</h6>
+            <p>
+            Applying the <a href="#LMA" class="inner-link">Law of Mass Action kynetics</a> (LMA) and some quasi-static approximations as before, we can obtain the following ODE model of the AHL-LuxR inducible system.
+            </p>
+            <table style="width:100%">
+            <tr>
+              <th><p>Variable</p></th>
+              <th><p>Biochemical species</p></th>
+              <th><p>Units</p></th>
+            </tr>
+             <tr>
+              <td><p>n<sub>1</sub></p></td>
+              <td><p>GFP protein</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>2</sub></p></td>
+              <td><p>LuxR protein</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>3</sub></p></td>
+              <td><p>Dimer of (R.A)<sub>2</sub></p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+            </tr>
+             <tr>
+              <td><p>n<sub>4</sub></p></td>
+              <td><p>AHL intracellular inducer</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>5</sub></p></td>
+              <td><p>AHL<sub>ext</sub> intracellular inducer</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+             <tr>
+              <td><p>n<sub>6</sub></p></td>
+              <td><p>Monomer (R.A)</p></td>
+              <td><p>Molecules</p></td>
+             </tr>
+          </table>
+          <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Biochemical species.</h6>
+      <a href="https://static.igem.org/mediawiki/2018/7/77/T--Valencia_UPV--luxR_luxI_eqUPV2018.png" data-lightbox="true">
+        <img src="https://static.igem.org/mediawiki/2018/7/77/T--Valencia_UPV--luxR_luxI_eqUPV2018.png" />
+        </a>
+        <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Model equations.</h6>
+        <p>
+        As we can see, the model has <b>five differential equations plus one algebraic equation</b>. This model does not describe cell growth, but it considers a <b>constant number of cells N</b>. This is because the measurements were taken in a bioreactor that has one influx with medium similiar to another efflux which washes the cells away. Both fluxes are proportional to the dilution rate, so the cell density is kept constant.
+        </p>
+        <p>
+        We have programmed a MATLAB function called <a href="https://static.igem.org/mediawiki/2018/1/16/T--Valencia_UPV--mi_luxUPV2018.txt" target="_blank"><b>mi_lux.m</b></a> for the ODE model, and also a MATLAB script called <a href="https://static.igem.org/mediawiki/2018/9/9b/T--Valencia_UPV--model_ind_luxUPV2018.txt" target="_blank"><b>model_lux.m</b></a> to define the parameters and simulate the model (<a href="https://www.mathworks.com/help/matlab/ref/ode15s.html" style="padding-right: 0" target="_blank">ode15s</a> MATLAB function).
+        </p>
+        <a href="https://static.igem.org/mediawiki/2018/6/69/T--Valencia_UPV--model_ind_lux_graphUPV2018.png" data-lightbox="true">
+        <img src="https://static.igem.org/mediawiki/2018/6/69/T--Valencia_UPV--model_ind_lux_graphUPV2018.png" />
+        </a>
+        <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model. Model predictions using parameter values from literature.</h6>
+        <a href="https://static.igem.org/mediawiki/2018/d/da/T--Valencia_UPV--ahl_gfp_graphUPV2018.png" data-lightbox="true">
+        <img src="https://static.igem.org/mediawiki/2018/d/da/T--Valencia_UPV--ahl_gfp_graphUPV2018.png" />
+        </a>
+        <h6 style="text-align: left; padding-left: 5em;">AHL-LuxR inducible model analysis. The graph shows the relation between AHL concentration and protein expression.</h6>
+        <p>
+        As we can see, the results show a <b>clear dependence between the expression of the protein and the inducing AHL concentration</b>. Comparing the experimental data (normalized for different AHL concentrations) with the simulated results, we can see that both closely match and this dynamics is the so-called <b>Hill function</b>.
+        </p>
+        <a class="anchorOffset" id="optimization"></a>
+        <h4>Multi-objective parameter optimization</h4>
+        <p>
+        <b>To what extent is our model valid? What values should the parameters take? To what extent do the theoretical results resemble the experimental ones? Is our model able to explain the behaviour of cells in reality?</b>
+        </p>
+        <p>
+        One of the most important phases in the field of Printeria Modeling has been the <b>validation of theoretical models</b> with experimental data. In the Printeria team we wanted to confirm that the models designed are consistent with our experiments. However, we know that the <b>parameters will not take a fixed value</b>, but vary depending on the genetic construction with which we experiment. With this idea in mind, the need to apply an optimization process arises.
+        </p>
+        <p>
+        The <b>multiobjective parameter optimization</b> process [<a href="#references" class="inner-link">3</a>]  minimizes two or more design objectives that have a trade-off between them. They are cost functions that depend on  some decision variables. In our case, <b>these objectives are estimation errors between experimental data and the model predictions</b>, whereas the <b>decission variables are some of our model parameters</b>. Using a mathematical algorithm to perform multiobjective optimization, we can find the <b>optimal solutions for the model parameters also known as Pareto Front</b>. The Pareto front has the optimal solutions that do not improve one objective without worsening the remaining objectives.
+        </p>
+        <p>
+        In multi-objective optimization, there is no single solution, but rather a set of them which form the <a href="https://static.igem.org/mediawiki/2018/a/ad/T--Valencia_UPV--pfrontUPV2018.png" target="_blank"><b>Pareto front</b></a>. For each of these solutions, we find a set of decision variables: the <a href="https://static.igem.org/mediawiki/2018/c/ce/T--Valencia_UPV--psetUPV2018.png" target="_blank"><b>Pareto set</b></a> [<a href="#references" class="inner-link">6</a>]. In our case, the Pareto front solutions represent the RMS error between experimental data and model predictions, and the Pareto set has the sets of parameters associated to one Pareto front solution.
+        </p>
+        <p>
+        The Printeria Modeling team has established a protocol to obtain the optimal solutions of the model parameters for any experiment:
+        </p>
+        <ol>
+          <li><p>
+            We define the <b>objectives to be optimized</b>. These will be the values of Fluorescence F/Unit of Absorbance OD or FOD, and the cellular growth (OD) of a Transcriptional Unit (TU). Therefore, if we have different <i>n</i> TU in an experiment, we will optimize <i>2n</i> objectives.
+          </p></li>
+          <li><p>
+            We choose the <b>parameters to optimize</b> and establish the range of values they can take.
+          </p></li>
+          <li><p>
+            We select the <b>identification and validation data</b>. The identification data are those used in the optimization process. The validation data are used to compare the experiment with the simulated theoretical model and the optimized parameters.
+          </p></li>
+          <li><p>
+            We define the <b>cost function</b>, which specifies the error function to be minimized. It simulates the model for different parameter values, and calculates the error between the simulation data and the experimental identification data.
+          </p></li>
+          <li><p>
+            The <b>mathematical optimization algorithm</b> is executed. In our case we use the <a href="https://es.mathworks.com/matlabcentral/fileexchange/39215-multi-objective-differential-evolution-algorithm-with-spherical-pruning" target="_blank" style="padding-right: 0">Multi-objective Differential Evolution Algorithm with Spherical Pruning</a>. This algorithm uses the cost function to test different parameter values and thus search for optimal parameter values.
+          </p></li>
+          <li><p>
+            The <b>Pareto set and Pareto front diagrams</b> and the different solutions of our optimized parameters for the different objectives are obtained.
+          </p></li>
+          <li><p>
+        <b>Decision Making</b> is carried out by the designer. The optimal parameters are chosen for our <i>2n</i> objectives.
+          </p></li>
+          <li><p>
+            <b>The model is simulated</b> with the optimized parameters <b>and compared</b> with the validation data.
+          </p></li>
+        </ol>
+        <p>
+        Following this protocol for each experiment, we have determined the best parameters for our models that fully fit the experimental data.
+        </p>
@@ Line 1,241: / Line 1,492: @@
-					<a class="anchorOffset" id="simtool"></a>
+          <a class="anchorOffset" id="simtool"></a>
                    <h3>Simulation Tool</h3>
                      <p>
-                     One of the main challenges of the Printeria project has been to give the user a chance to really understand what our device is doing when it prints genetic circuits on bacteria.  Facing this challenge, we have also sought to provide as much information as possible about the Printeria product. <b>And what better way than to give our user a quantitative, mathematical description of what happens in our cells?</b>
+                     One of the main challenges of Printeria has been to give the user a chance to really understand what our device is doing when it prints genetic circuits on bacteria.  So we have also sought to provide as much information as possible about the Printeria product. <b>And what better way than to give our user a quantitative, mathematical description of what happens in our cells?</b>
                      </p>
                      <p>
@@ Line 1,252: / Line 1,503: @@
                      </p>
                      <p>
-                     Our Simulation Tool has been conceived as a <b>mathematical model simulation program</b> that has been <b>perfectly integrated into our <a href="" target="_blank">Printeria Controller</a> software</b>. When our user wants to assemble a genetic construct and selects the parts, the Simulation Tool offers the possibility to <b>experiment <i>in silico</i></b> and predict cell behavior before printing the bacteria. All this, just by pressing the <b><i>Show model results</i></b> button... and instantly!
+                     Our Simulation Tool has been conceived as a <b>mathematical model simulation program</b> that has been <b>perfectly integrated into our <a href="159.203.181.207:3000" target="_blank">Printeria Controller</a> software</b>. When our user wants to assemble a genetic construct and selects the parts, the Simulation Tool offers the possibility to <b>experiment <i>in silico</i></b> and predict cell behavior before printing the bacteria. All this, just by pressing the <b><i>Show model results</i></b> button... and instantly!
                      </p>
                      <p><b>But how does the Simulation Tool work?</b></p>
                      <p>
-                     The Printeria Modeling and Software teams have jointly designed a program developed in <b>a single Python script</b> (have a look at our <a href="" target="_blank"><b>simulate.py</b></a> script). The program combines the functions of the main mathematical models of Printeria with the information of the Printeria kit stored in the <a href="" target="_blank"><b> Printeria database</b></a>. In addition, as it is a single Python file, it is stored and run on the <a href="" target="_blank"><b>Raspberry Pi 3 server</b></a>.
+                     The Printeria Modeling and Software teams have jointly designed a program developed in <b>a single Python script</b> (have a look at our <a href="https://static.igem.org/mediawiki/2018/a/a3/T--Valencia_UPV--simulate_pyUPV2018.txt" target="_blank"><b>simulate.py</b></a> script). The program combines the functions of the main mathematical models of Printeria with the information of the Printeria kit stored in the <a href="https://2018.igem.org/Team:Valencia_UPV/Software#flow" target="_blank"><b>Printeria database</b></a>. In addition, as it is a single Python file, it is stored and run on the Raspberry Pi 3 server.
                      </p>
                      <p><b>Now let's see what happens if the user has chosen the Printeria parts and presses the Simulate button...</b></p>
                      <a href="https://static.igem.org/mediawiki/2018/2/2b/T--Valencia_UPV--simtool_esqUPV2018.png" data-lightbox="true">
-						<img src="https://static.igem.org/mediawiki/2018/2/2b/T--Valencia_UPV--simtool_esqUPV2018.png" />
+                      <img src="https://static.igem.org/mediawiki/2018/2/2b/T--Valencia_UPV--simtool_esqUPV2018.png" />
-					</a>
+                    </a>
+                    <h6 style="text-align: left; padding-left: 5em;">Simulation Tool working scheme.</h6>
                      <ol>
-                    	<li><p>
+                      <li><p>
-                    		The <b>Printeria client connects to the <a href="" target="_blank">Printeria MongoDB database</a></b> where we store all the information of our Printeria kit.
+                        The <b>Printeria client connects to the Printeria database (MongoDB)</b> where we store all the information of our Printeria kit.
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-							The <b>four parts of the genetic construction (promoter, RBS, CDS and transcriptional terminator) are extracted</b> from the database thanks to their identifiers.
+              The <b>four parts of the genetic construction (promoter, RBS, CDS and transcriptional terminator) are extracted</b> from the database thanks to their identifiers.
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							The <b>type of model</b> (constitutive or inducible expression) is identified from the type of promoter selected.
+              The <b>type of model</b> (constitutive or inducible expression) is identified from the type of promoter selected.
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							The <b>model parameters</b> of each construction part are extracted.
+              The <b>model parameters</b> of each construction part are extracted.
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							The <b>initial conditions</b> of the simulation and its <b>duration</b> are established.
+              The <b>initial conditions</b> of the simulation and its <b>duration</b> are established.
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							The <b>model is simulated</b> using Python's <a href="https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html" target="_blank" style="padding-right: 0">odeint function</a>
+              The <b>model is simulated</b> using Python's <a href="https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html" target="_blank" style="padding-right: 0">odeint function</a>
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							A temporary <b>CSV file</b> is generated in which the <b>we store the results of the simulation</b> in a certain format.
+              A temporary <b>CSV file</b> is generated in which the <b>we store the results of the simulation</b> in a certain format.
-						</p></li>
+            </p></li>
-						<li><p>
+            <li><p>
-							From the CSV file, the <b>simulation results are represented graphically</b> on the Printeria site. The user can <b>view or download</b> their results.
+              From the CSV file, the <b>simulation results are represented graphically</b> on the Printeria site. The user can <b>view or download</b> their results.
-						</p></li>
+            </p></li>
                      </ol>
                      <p><b>And what are the advantages of an application like our Simulation Tool?</b></p>
                      <ul>
-                    	<li><p>
+                      <li><p>
-                    		<b>User-friendly</b>. It is very simple to operate for the user. Just select your Printeria parts, press a button... And that's it!
+                        <b>User-friendly</b>. It is very simple to operate for the user. Just select your Printeria parts, press a button... And that's it!
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-                    		<b>Integrated</b>. All our software is included in the Raspberry Pi 3 server. You don't need to download the program.
+                        <b>Integrated</b>. All our software is included in the Raspberry Pi 3 server. You don't need to download the program.
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-                    		<b>Instant experimental data</b>. Our Simulation Tool runs simulations at high speed. In a few seconds you'll have your results.
+                        <b>Instant experimental data</b>. Our Simulation Tool runs simulations at high speed. In a few seconds you'll have your results.
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-                    		<b>Customizable parameters</b>. You can modify your parameters and adapt them to your experiment, to obtain more precise results.
+                        <b>Customizable parameters</b>. You can modify your parameters and adapt them to your experiment, to obtain more precise results.
-                    	</p></li>
+                      </p></li>
-                    	<li><p>
+                      <li><p>
-                    		<b>All-in-one</b>. Our Simulation Tool includes several mathematical models, constitutive and inducible, in a single code and solves them particularizing for each Printeria genetic construction.
+                        <b>All-in-one</b>. Our Simulation Tool includes several mathematical models, constitutive and inducible, in a single code and solves them particularizing for each Printeria genetic construction.
-                    	</p></li>
+                      </p></li>
                      </ul>
                      <p>
-                     <b>Would you like to try the Simulation Tool?</b> Go to our <a href="" target="_blank">Printeria Controller </a> site and discover all the possibilities offered by our software.
+                     <b>Would you like to try the Simulation Tool?</b> Go to our <a href="159.203.181.207:3000" target="_blank">Printeria Controller </a> site and discover all the possibilities offered by our software.
                      </p>
                      <p><b>
                      What are you waiting for to start discovering it?
                      </b></p>
+               </div>
+            </div>
+         </div>
+                  <a class="anchorOffset" id="references"></a>
-                   <a class="anchorOffset" id="references"></a>
                    <h3>References</h3>
                    <ol class="references">
-                  	<li><p>
+                    <li><p><a class="anchorOffset" id="references1"></a>
-                  		Picó, J., Vignoni, A., Picó-Marco, E., & Boada, Y. (2015). Modelado de sistemas bioquímicos: De la ley de acción de masas a la aproximación lineal del ruido. Revista Iberoamericana de Automática e Informática Industrial RIAI, 12(3), 241-252.
+                      Picó, J., Vignoni, A., Picó-Marco, E., & Boada, Y. (2015). <i>Modelado de sistemas bioquímicos: De la ley de acción de masas a la aproximación lineal del ruido.</i> Revista Iberoamericana de Automática e Informática Industrial RIAI, 12(3), 241-252.
-                  	</p></li>
+                    </p></li>
-                  	<li><p>
+                    <li><p><a class="anchorOffset" id="references2"></a>
-                  		Segel, L. A., & Slemrod, M. (1989). The quasi-steady-state assumption: a case study in perturbation. SIAM review, 31(3), 446-477.
+                      Y. Boada, A. Vignoni, and J. Picó. (2017). <i>Engineered control of genetic variability reveals interplay among quorum sensing, feedback regulation, and biochemical noise</i>. ACS Synthetic Biology, 6(10):1903–1912, 2017a.
-                  	</p></li>
+                    </p></li>
-                  	<li><p>
+                    <li><p><a class="anchorOffset" id="references3"></a>
-                  		Boada, Y., Vignoni, A., Reynoso-Meza, G., & Picó, J. (2016). Parameter identification in synthetic biological circuits using multi-objective optimization. Ifac-Papersonline, 49(26), 77-82.
+                      Segel, L. A., & Slemrod, M. (1989). <i>The quasi-steady-state assumption: a case study in perturbation.</i> SIAM review, 31(3), 446-477.
-                  	</p></li>
+                    </p></li>
-                  	<li><p>
+                    <li><p><a class="anchorOffset" id="references4"></a>
-                  		Boada, Y., Vignoli, A., & Picó, J. (2017). Reduction of population variability in protein expression: A control engineering approach. Actas de las XXXVIII Jornadas de Automática.
+                      Boada, Y., Vignoni, A., Reynoso-Meza, G., & Picó, J. (2016).<i> Parameter identification in synthetic biological circuits using multi-objective optimization</i>. Ifac-Papersonline, 49(26), 77-82.
-                  	</p></li>
+                    </p></li>
-                  	<li><p>
+                    <li><p><a class="anchorOffset" id="references5"></a>
-                  		Schleif, R. (2000). Regulation of the L-arabinose operon of Escherichia coli. Trends in Genetics, 16(12), 559-565.
+                       R. Milo and R. Phillips. <i>Cell Biology by the Numbers</i>. First edition, 2015. ISBN9780815345374.
-                  	</p></li>
+                    </p></li>
-                  	<li><p>
+                    <li><p>
-                  		Tesis Yadira
+                      Boada, Y., Vignoni, A., & Picó, J. (2017). <i>Reduction of population variability in protein expression: A control engineering approach.</i> Actas de las XXXVIII Jornadas de Automática.
-                  	</p></li>
+                    </p></li>
+                    <li><p><a class="anchorOffset" id="references7"></a>
+                        U. Alon. An Introduction to Systems Biology. <i>Desing Principles of Biological Circuits</i>. Champan and Hall/CRC, Edition, 2007.
+                    </p></li>
+                    <li><p><a class="anchorOffset" id="references8"></a>
+                      Schleif, R. (2000). <i>Regulation of the L-arabinose operon of Escherichia coli.</i> Trends in Genetics, 16(12), 559-565.
+                    </p></li>
+                    <li><p><a class="anchorOffset" id="references9"></a>
+                      Boada, Y. (2018). <i>A systems engineering approach to model, tune and test synthetic gene circuits.</i> PhD. Thesis, Universitat Politècnica de València.
+                    </p></li>
+                    <li><p><a class="anchorOffset" id="references10"></a>
+                      N. E. Buchler, U. Gerland, and T. Hwa. <i>Nonlinear protein degradation and the function of genetic circuits</i>. Proceedings of the National Academy of Sciences of the United States of America, 102(27):9559–9564, 2005.
+                    </p></li>
                    </ol>
-               </div>
-            </div>
-         </div>
        </div>
     </div>

Difference between revisions of "Team:Valencia UPV/Model"

Latest revision as of 02:22, 18 October 2018

Index

Models & Experiments

Modeling process

Modeling process schema.

Constitutive expression models

Model design

Constitutive expression model. Cell schema.

Constitutive expression model. Biochemical reactions.

Constitutive expression model. Model parameters obtained from literature.

Constitutive expression model. Biochemical species.

Constitutive expression model. Model equations.

Constitutive expression model. Model predictions using parameter values from literature.

Constitutive expression model analysis. The graph represents de PoI stationary value as function of CR and p ratios.

Experiments & Optimization

Biotek Cytation 3 experimental parameters.

Optimization specifications for the experiment.

Experiment 1 changing RBS. Experimental and optimized simulated model data of strong, medium and weak protein expression RBS

Experiment 2 changing RBS. Experimental and optimized simulated model data of strong and very weak protein expression RBS

Experiment 2 changing RBS. Experimental and optimized simulated model data of very weak protein expression RBS

List of optimized parameters for RBS experiment.

Relative strength between different RBS parts.

Biotek Cytation 3 experimental parameters.

Optimization specifications for the experiment.

Experiment 1 changing promoters. Experimental and optimized simulated model data of strong, medium and weak promoters.

List of optimized parameters for promoters experiment.

Relative strength between different promoter parts.

Biotek Cytation 3 experimental parameters.

Optimization specifications for the experiment.

Experiment YFP vs. YFP tag. Experimental data and optimized model of the YFP and YFP tag proteins

List of optimized parameters.

Inducible expression models

PBAD/araC inducible model

Model design

PBAD/araC inducible model. Cell schema.

PBAD/araC inducible model. Biochemical reations.

PBAD/araC inducible model. Model parameters.

PBAD/araC inducible model. Biochemical species.

PBAD/araC inducible model. Model equations.

PBAD/araC inducible model. Model predictions using parameter values from literature.

PBAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p and K ratios.

PBAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p ratio and L-arabinose concentration (arab0).

AHL-LuxR inducible model

Model design

AHL-LuxR inducible model. Cell schema.

AHL-LuxR inducible model. Biochemical reactions.

AHL-LuxR inducible model. Model parameters.

AHL-LuxR inducible model. Biochemical species.

AHL-LuxR inducible model. Model equations.

AHL-LuxR inducible model. Model predictions using parameter values from literature.

AHL-LuxR inducible model analysis. The graph shows the relation between AHL concentration and protein expression.

Multi-objective parameter optimization

Simulation Tool

Simulation Tool working scheme.

References

Constitutive expression model analysis. The graph represents de PoI stationary value as function of C_R and p ratios.

P_BAD/araC inducible model

P_BAD/araC inducible model. Cell schema.

P_BAD/araC inducible model. Biochemical reations.

P_BAD/araC inducible model. Model parameters.

P_BAD/araC inducible model. Biochemical species.

P_BAD/araC inducible model. Model equations.

P_BAD/araC inducible model. Model predictions using parameter values from literature.

P_BAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p and K ratios.

P_BAD/araC inducible model analysis. The graph represents de PoI stationary value as function of p ratio and L-arabinose concentration (arab₀).