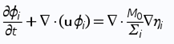| Line 434: | Line 434: | ||
</div> | </div> | ||
<div> | <div> | ||
| − | + | <h1>Background</h1> | |
<h2>Phase-field modeling overview</h2> | <h2>Phase-field modeling overview</h2> | ||
| − | <p>Phase-field models are mathematical models used for solving interfacial problems. They are based on the generalized free-energy functional approach (lattice Boltzmann), meaning that the system evolution is driven by the minimisation of free energy. Important thing to note is that sharp fluid interfaces in the models are replaced by a thin transition region where the interfacial forces are distributed in a smooth manner. This provides model an easy treatment of topological variations at the interface1. In order to describe phases in numerical form, equations use phase variables | + | <p>Phase-field models are mathematical models used for solving interfacial problems. They are based on the generalized free-energy functional approach (lattice Boltzmann), meaning that the system evolution is driven by the minimisation of free energy. Important thing to note is that sharp fluid interfaces in the models are replaced by a thin transition region where the interfacial forces are distributed in a smooth manner. This provides model an easy treatment of topological variations at the interface1. In order to describe phases in numerical form, equations use phase variables ϕ. In three-phase systems, phase variables are described as ϕi , where i = A, B, C, and the variable is equal to 1 in the phase i and 0 outside.</p> |
<p>Typically used phase-field models for two and three phase fluid systems couple fourth order nonlinear advection-diffusion equations, called Cahn-Hilliard equations, which represent the evolution of the phase variables with the Navier-Stokes equations for the fluid motion 2 . Equations (1), (2) and (3) form the traditional Cahn-Hilliard equation, and Eq. (4) is Navier-Stokes equation - both of them are used in our calculations on COMSOL</p> | <p>Typically used phase-field models for two and three phase fluid systems couple fourth order nonlinear advection-diffusion equations, called Cahn-Hilliard equations, which represent the evolution of the phase variables with the Navier-Stokes equations for the fluid motion 2 . Equations (1), (2) and (3) form the traditional Cahn-Hilliard equation, and Eq. (4) is Navier-Stokes equation - both of them are used in our calculations on COMSOL</p> | ||
| − | <p> | + | <p> <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/f/fe/T--Vilnius-Lithuania--dv_eq1_Model.png"></div> |
</p> | </p> | ||
| − | <p> | + | <p> <div class="image-container"> <img src="https://static.igem.org/mediawiki/2018/f/fe/T--Vilnius-Lithuania--dv_eq2_Model.png"></div> |
</p> | </p> | ||
| − | <p> | + | <p> <div class="image-container"> <img src="https://static.igem.org/mediawiki/2018/c/c8/T--Vilnius-Lithuania--dv_eq3_Model.png"></div> |
</p> | </p> | ||
| − | <p> | + | <p> <div class="image-container"> <img src="https://static.igem.org/mediawiki/2018/f/fb/T--Vilnius-Lithuania--dv_eq4_Model.png"></div> |
</p> | </p> | ||
<p>M0 is the mobility tuning parameter that determines the relaxation time of interface and the time scale of diffusion in C-H equation. It should be noted, that interfacial diffusion (the Gibbs-Thomson effect) is inevitable in phase phase field method because the diffusion term is used in the right side of Eq. (1). Due to this, prolonged simulations of our system result in spheres diffusing and constantly changing their size (Fig. 1.). Because of that, we have chosen to analyze only the first few spheres formed in every simulation as their size proved to be most accurate.</p> | <p>M0 is the mobility tuning parameter that determines the relaxation time of interface and the time scale of diffusion in C-H equation. It should be noted, that interfacial diffusion (the Gibbs-Thomson effect) is inevitable in phase phase field method because the diffusion term is used in the right side of Eq. (1). Due to this, prolonged simulations of our system result in spheres diffusing and constantly changing their size (Fig. 1.). Because of that, we have chosen to analyze only the first few spheres formed in every simulation as their size proved to be most accurate.</p> | ||
| − | <p> | + | <p>ϵ (interface thickness parameter) is also an important parameter as it defines the width of transition between phases and affects both the surface tension force and the relaxation time of interface. Usually it is compared to the characteristic length of the system and must be chosen small enough to depict interface changes accurately, yet too small of a thickness shall cause instabilities in calculations.</p> |
| − | <p>Most of the time the model can be described with several dimensionless parameters, such as capillary number calculated for the continuous phase, Ca = | + | <p>Most of the time the model can be described with several dimensionless parameters, such as capillary number calculated for the continuous phase, Ca =μcvc/γ, the Reynolds number Re =ρvcL/μc, the viscosity ratio λ=μd/μc, and the flow rate ratio Q=vd/vc 3. In our model Reynolds number is small (Re < 1) and does not influence droplet size, so we mainly focus on Ca, λ and Q and consider the influence of the latter two on the liposome formation. |
</p> | </p> | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/e/ed/T--Vilnius-Lithuania--dv_fig1a_Model.gif"></div> |
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/9/99/T--Vilnius-Lithuania--dv_fig1b_Model.gif"></div> |
<strong>Fig. 1</strong> Visual comparison of modeled and real life liposome formation process. A slight diffusion is observed in a model due to the diffusion term in P-H equations, which makes long simulations unreliable. In the plot, phase variables A, B and C have values of 1 (blue), 2 (green) and 3 (red) respectively. | <strong>Fig. 1</strong> Visual comparison of modeled and real life liposome formation process. A slight diffusion is observed in a model due to the diffusion term in P-H equations, which makes long simulations unreliable. In the plot, phase variables A, B and C have values of 1 (blue), 2 (green) and 3 (red) respectively. | ||
| Line 465: | Line 465: | ||
</ol> | </ol> | ||
</p> | </p> | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/a/a3/T--Vilnius-Lithuania--dv_fig2_Model.png"></div> |
<strong>Fig. 2</strong> Original 3D junction geometry extracted from the CAD file. Because of its size, it is too inefficient to simulate this whole piece of device. | <strong>Fig. 2</strong> Original 3D junction geometry extracted from the CAD file. Because of its size, it is too inefficient to simulate this whole piece of device. | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/6/6a/T--Vilnius-Lithuania--dv_fig3_Model.png"></div> |
<strong>Fig. 3</strong> Minimized geometry with main measurements and boundaries described, used in all simulations. The inflow rates of LO and OA phases are divided by 2, because their channels split into two in order to press the stream of IA phase in junction. | <strong>Fig. 3</strong> Minimized geometry with main measurements and boundaries described, used in all simulations. The inflow rates of LO and OA phases are divided by 2, because their channels split into two in order to press the stream of IA phase in junction. | ||
<h2>Mesh</h2> | <h2>Mesh</h2> | ||
| − | <p>For solving the model we used finite element method, which divides geometry into small mesh elements, where partial differential equations are solved. Interface capturing method incorporated in it keeps the mesh fixed and the boundary discontinuities are smeared out over the finite width | + | <p>For solving the model we used finite element method, which divides geometry into small mesh elements, where partial differential equations are solved. Interface capturing method incorporated in it keeps the mesh fixed and the boundary discontinuities are smeared out over the finite width ϵ 3,4. To successfully capture interface movement between different phases, mesh size should be small enough, but not too small, as every single element adds more time to computing and quality of the results stops improving substantially at a certain point.</p> |
<p>Most of the time we only control the size of mesh elements. For our channel domains a predefined normal sized mesh was used, as they only contained one phase and interface problems did not occur there. For junction and post-junction parts, a predefined extra fine mesh was used with maximum element size value set to 1µm, which is 1/10 size of a smallest expected droplet and also 1/10 of our characteristic length, which has been chosen to be the width of horizontal IA channel (Fig. 4)</p> | <p>Most of the time we only control the size of mesh elements. For our channel domains a predefined normal sized mesh was used, as they only contained one phase and interface problems did not occur there. For junction and post-junction parts, a predefined extra fine mesh was used with maximum element size value set to 1µm, which is 1/10 size of a smallest expected droplet and also 1/10 of our characteristic length, which has been chosen to be the width of horizontal IA channel (Fig. 4)</p> | ||
| − | <a img | + | <a img > |
<strong>Fig. 4</strong> Generated mesh used in all simulations. Refined grid in junction and post-junction helps with realistic interface capturing. | <strong>Fig. 4</strong> Generated mesh used in all simulations. Refined grid in junction and post-junction helps with realistic interface capturing. | ||
<p></p> | <p></p> | ||
| Line 484: | Line 484: | ||
<tr> | <tr> | ||
<th><strong>Phase</strong></th> | <th><strong>Phase</strong></th> | ||
| − | <th><Strong>Density | + | <th><Strong>Density ρ(kg/m3) </Strong></th> |
<th><Strong>Dynamic viscosity µ (Pa*s)</Strong></th> | <th><Strong>Dynamic viscosity µ (Pa*s)</Strong></th> | ||
<th><Strong>Real composition</Strong></th> | <th><Strong>Real composition</Strong></th> | ||
| Line 516: | Line 516: | ||
<h1>Description of the System</h1> | <h1>Description of the System</h1> | ||
<p>Fig. 3 shows our flow focusing model configuration with boundaries specified. There is one main inlet for IA phase, and two for each LO and OA phases on the left side. On the right side, there is an outlet with outflow pressure set to p = 0. For laminar flow, wall condition is set to no slip, which states that the flow velocity at the walls is always v = 0 and it gives a good approximation of the whole system.</p> | <p>Fig. 3 shows our flow focusing model configuration with boundaries specified. There is one main inlet for IA phase, and two for each LO and OA phases on the left side. On the right side, there is an outlet with outflow pressure set to p = 0. For laminar flow, wall condition is set to no slip, which states that the flow velocity at the walls is always v = 0 and it gives a good approximation of the whole system.</p> | ||
| − | <p>In experimental set-up, we coat the OA channels, junction and post-junction with PVA to make it hydrophilic, contrary to hydrophobic PDMS, which is the material of which the microfluidic devices are made. This provides a good setting for liposome formation5, and we take that into account by adjusting contact angles at the wetted walls for ternary phase field node. With respect to model limitations (nukreipia | + | <p>In experimental set-up, we coat the OA channels, junction and post-junction with PVA to make it hydrophilic, contrary to hydrophobic PDMS, which is the material of which the microfluidic devices are made. This provides a good setting for liposome formation5, and we take that into account by adjusting contact angles at the wetted walls for ternary phase field node. With respect to model limitations (nukreipia į skiltį limitations), all the contact angles in IA and LO channels are set to 90 degrees. In the coated side, we assume phase OA has a perfect wetting condition on the channel walls against both IA and LO phases, while the contact angle between the latter two is set at 30 degrees. |
</p> | </p> | ||
| − | <p>The aforementioned interface thickness parameter | + | <p>The aforementioned interface thickness parameter ϵ is set to 1.4 µm as it is the lowest stable value regarding our mesh and mobility tuning parameter, though it is more than enough to accurately depict the results of simulations. Surface tension is another important aspect to be considered and it is set to σ = 0.0085 N/m, which is an interfacial tension between octanol and water 6, for all three interfaces between phases (<strong>See Limitations</strong>).</p> |
<p>In order to make our model as realistic as possible, several other parameters are taken from a single baseline wet lab experiment with similar materials and geometry as mentioned before.</p> | <p>In order to make our model as realistic as possible, several other parameters are taken from a single baseline wet lab experiment with similar materials and geometry as mentioned before.</p> | ||
<p>Flow rates are transformed into flow velocities for COMSOL and calculated as described in Tab. 2.</p> | <p>Flow rates are transformed into flow velocities for COMSOL and calculated as described in Tab. 2.</p> | ||
| Line 527: | Line 527: | ||
<tr> | <tr> | ||
<th><strong>Channel</strong></th> | <th><strong>Channel</strong></th> | ||
| − | <th><Strong>Inlet area(µm<sup>2</sup>) | + | <th><Strong>Inlet area(µm<sup>2</sup>) ρ(kg/m3) </Strong></th> |
<th><Strong>Flow rate(µL/h)</Strong></th> | <th><Strong>Flow rate(µL/h)</Strong></th> | ||
<th><Strong>Flow velocity (m/s)</Strong></th> | <th><Strong>Flow velocity (m/s)</Strong></th> | ||
| Line 556: | Line 556: | ||
<p>Mobility parameter in this model is crucial. As its value becomes higher, droplet size in micro-channel increases. This can be explained by the parameters’ mathematical function - raising values causes the increase in interface relaxation time, meaning the diffusion gets stronger as well <sup>1</sup>>. So we have compared the numerical and experimental results of liposome synthesis (Fig. 5) and approximated our characteristic mobility tuning parameter to be M<sup>0</sup> = 2E-12 m<sup>3</sup>>/s. The diameter of the droplet with this value was 12.1µm, which is a close match to the real size. | <p>Mobility parameter in this model is crucial. As its value becomes higher, droplet size in micro-channel increases. This can be explained by the parameters’ mathematical function - raising values causes the increase in interface relaxation time, meaning the diffusion gets stronger as well <sup>1</sup>>. So we have compared the numerical and experimental results of liposome synthesis (Fig. 5) and approximated our characteristic mobility tuning parameter to be M<sup>0</sup> = 2E-12 m<sup>3</sup>>/s. The diameter of the droplet with this value was 12.1µm, which is a close match to the real size. | ||
</p> | </p> | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/d/d9/T--Vilnius-Lithuania--dv_fig5a_Model.png"></div> |
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/4/4a/T--Vilnius-Lithuania--dv_fig5b_Model.png"></div> |
<strong>Fig. 5</strong> A comparison between a modeled baseline experiment and actual view of the junction. Both of them produce vesicles of around 12 µm, though slight variations occur in real setting due to unsteady flow caused by micro-pumps. Results of both systems concur well enough to assume that our model setup is reliable and close to reality. | <strong>Fig. 5</strong> A comparison between a modeled baseline experiment and actual view of the junction. Both of them produce vesicles of around 12 µm, though slight variations occur in real setting due to unsteady flow caused by micro-pumps. Results of both systems concur well enough to assume that our model setup is reliable and close to reality. | ||
| Line 564: | Line 564: | ||
<h2>Parametric sweeps and example of liposome radius calculation</h2> | <h2>Parametric sweeps and example of liposome radius calculation</h2> | ||
<p>In order to investigate how our system depends on certain parameters, we have performed parametric sweeps on every one of these parameters separately. By doing so, COMSOL Multiphysics resolved our model with every parametric value specified automatically and stored the results under a single node. | <p>In order to investigate how our system depends on certain parameters, we have performed parametric sweeps on every one of these parameters separately. By doing so, COMSOL Multiphysics resolved our model with every parametric value specified automatically and stored the results under a single node. | ||
| − | To find out the size of the liposomes, the first fully formed droplet was taken and 2D cut line data set was created going through the middle of the sphere in y-axis direction (Fig. 6). Next, the variation of phase variable C (which stands for our IA phase) was extracted from the data set and results were depicted in graphs. The exact point of phase edge for all studies performed has been assumed as | + | To find out the size of the liposomes, the first fully formed droplet was taken and 2D cut line data set was created going through the middle of the sphere in y-axis direction (Fig. 6). Next, the variation of phase variable C (which stands for our IA phase) was extracted from the data set and results were depicted in graphs. The exact point of phase edge for all studies performed has been assumed as ϕc = 0.5.</p> |
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/5/59/T--Vilnius-Lithuania--dv_fig6_Model.png"></div> |
| − | <strong>Fig. 6</strong> An example of data sets analysed (yellow line in Fig.). One fully formed sphere for every parametric sweep step was measured by extracting | + | <strong>Fig. 6</strong> An example of data sets analysed (yellow line in Fig.). One fully formed sphere for every parametric sweep step was measured by extracting ϕc values from similar linear data sets. |
<p></p> | <p></p> | ||
| − | <h2>Liposome size dependence on viscosity ratio | + | <h2>Liposome size dependence on viscosity ratio λ </h2> |
| − | <p>First of all, the impact of IA and OA phase viscosity ratio ( | + | <p>First of all, the impact of IA and OA phase viscosity ratio ( λ = µ<sub>IA</sub>/µ<sub>OA</sub>) was investigated. Studies suggest, that increasing λ also increases the generated droplet size 7. Though the changes are more significant in high capillary numbers, where droplet formation is driven by viscosity. In our case, the capillary number was relatively small (Ca ≈ 0.034), so the flow was more surface tension-dominated. |
The simulation was run with a set of different OA phase dynamic viscosity values (Tab. 3.) and results are presented in Fig. 7 and Fig. 8.</p> | The simulation was run with a set of different OA phase dynamic viscosity values (Tab. 3.) and results are presented in Fig. 7 and Fig. 8.</p> | ||
| Line 580: | Line 580: | ||
<th><Strong>OA dynamic viscosity µ<sub>OA</sub> (Pa*s) | <th><Strong>OA dynamic viscosity µ<sub>OA</sub> (Pa*s) | ||
</Strong></th> | </Strong></th> | ||
| − | <th><Strong>Viscosity ratio | + | <th><Strong>Viscosity ratio λ</Strong></th> |
</tr> | </tr> | ||
| Line 626: | Line 626: | ||
</table> | </table> | ||
<p></p> | <p></p> | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/7/74/T--Vilnius-Lithuania--dv_fig7_Model.png"></div> |
| − | <strong>Fig. 7</strong>Sphere radius dependency on viscosity ratio | + | <strong>Fig. 7</strong>Sphere radius dependency on viscosity ratio λ. Graph shows the simulated results of liposome radius for every given viscosity parameter, which here are depicted as ratio between viscosities of IA and OA phases. In our simulated range of parameters the radius varies from 5.08 µm to 6.75 µm. |
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/d/df/T--Vilnius-Lithuania--dv_fig8_Model.png"></div> |
| − | <strong>Fig. 8</strong> Sphere diameter dependence on viscosity ratio | + | <strong>Fig. 8</strong> Sphere diameter dependence on viscosity ratio λ. Simplified graph shows that sphere size increases linearly up until λ = 1 and viscosity regulation above this value results in less changes. |
| − | <p>As we see, droplet size increases almost linearly up to | + | <p>As we see, droplet size increases almost linearly up to λ = 0.996, meaning that increasing viscosity of OA phase leads to formation of smaller liposomes. However, it should be noted that by increasing viscosity in real life, we may encounter other problems, such as impeded droplet formation or liposomes bursting due to differences in osmotic pressure between inside and outside environments. Given these limitations, we can still effectively control our liposome size in about 1µm range. <var>Thus, we can conclude that viscosity ratio, while having a moderate effect, is still not a decisive parameter in vesicle size determination.</var></p> |
<h2>Liposome size dependency on velocity ratio V</h2> | <h2>Liposome size dependency on velocity ratio V</h2> | ||
| Line 695: | Line 695: | ||
</tbody> | </tbody> | ||
</table> | </table> | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/4/40/T--Vilnius-Lithuania--dv_fig9_Model.png"></div> |
| − | <strong>Fig. 9</strong> Sphere radius dependency on flow rate ratio Q. It should be noted that x-axis doesn’t start from zero in order to distinguish between first three values. In comparison with | + | <strong>Fig. 9</strong> Sphere radius dependency on flow rate ratio Q. It should be noted that x-axis doesn’t start from zero in order to distinguish between first three values. In comparison with λ, Q seems to affect liposome radius at a greater magnitude. In our simulated range of parameters the radius varies from 6.05 µm to 8.56 µm. |
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/8/80/T--Vilnius-Lithuania--dv_fig10_Model.png"></div> |
<strong>Fig. 10</strong> Sphere diameter dependency on flow rate ratio Q. Simplified graph shows that liposome diameter variation range is 5.5 µm in our configurations, which can be considered good enough for fine-tuning. | <strong>Fig. 10</strong> Sphere diameter dependency on flow rate ratio Q. Simplified graph shows that liposome diameter variation range is 5.5 µm in our configurations, which can be considered good enough for fine-tuning. | ||
| Line 705: | Line 705: | ||
<p>In contrary to dynamic viscosity ratio variation, flow rate ratio can be experimentally modified in a broad range of values, meaning we can effectively synthesize liposomes from 12 µm to around 17 µm with our current set-up. Nevertheless, we have found that when Q = 0.7, spheres cannot form anymore, as the OA phase cannot cut the stream of IA phase and it transforms into a continuous flow (Fig. 11). Therefore, Q = 0.7 is the critical value for liposome synthesis in our system. <var>In conclusion, the regulation of IA phase flow rate gives us an effective and fast method to vary the size of our liposomes in a range of few micrometers. | <p>In contrary to dynamic viscosity ratio variation, flow rate ratio can be experimentally modified in a broad range of values, meaning we can effectively synthesize liposomes from 12 µm to around 17 µm with our current set-up. Nevertheless, we have found that when Q = 0.7, spheres cannot form anymore, as the OA phase cannot cut the stream of IA phase and it transforms into a continuous flow (Fig. 11). Therefore, Q = 0.7 is the critical value for liposome synthesis in our system. <var>In conclusion, the regulation of IA phase flow rate gives us an effective and fast method to vary the size of our liposomes in a range of few micrometers. | ||
</var> </p> | </var> </p> | ||
| − | + | <div class="image-container"> <img src="https://static.igem.org/mediawiki/2018/4/49/T--Vilnius-Lithuania--dv_fig11_Model.png"></div> | |
<strong>Fig. 11</strong>Liposomes stop forming in our system when Q > 0.7, or V > 1 ( v<sub>IA</sub>/v<sub>OA</sub>). It means that in given dimensions, these values are critical for vesicle formation. | <strong>Fig. 11</strong>Liposomes stop forming in our system when Q > 0.7, or V > 1 ( v<sub>IA</sub>/v<sub>OA</sub>). It means that in given dimensions, these values are critical for vesicle formation. | ||
| Line 767: | Line 767: | ||
</table> | </table> | ||
| − | + | <div class="image-container"> <img src="https://static.igem.org/mediawiki/2018/5/5f/T--Vilnius-Lithuania--dv_fig12_Model.png"></div> | |
<strong>Fig. 12 </strong> Sphere radius dependency on IA channel width. Changes in IA channel width seem to cause greatest impact to the output. By increasing it by 5µm, liposome radius grows by 2.86µm. | <strong>Fig. 12 </strong> Sphere radius dependency on IA channel width. Changes in IA channel width seem to cause greatest impact to the output. By increasing it by 5µm, liposome radius grows by 2.86µm. | ||
| − | < | + | <div class="image-container"><img src="https://static.igem.org/mediawiki/2018/c/c2/T--Vilnius-Lithuania--dv_fig13_Model.png"></div> |
<strong>Fig. 13</strong> Sphere diameter dependency on IA channel width. Simplified graph shows an explicit tendency of liposome growth with increased width parameter. This implies that increasing or reducing the parameter should affect our system in a highly predictable manner. | <strong>Fig. 13</strong> Sphere diameter dependency on IA channel width. Simplified graph shows an explicit tendency of liposome growth with increased width parameter. This implies that increasing or reducing the parameter should affect our system in a highly predictable manner. | ||
<p>As we can see, channel width has a huge impact on the size of liposomes. Even by keeping flow rates of all phases the same, droplet radius variations depend solely on channel dimensions. We have tested channels from 10 µm to 15 µm, but other widths should also comply with given results and the only limit on minimal channel dimensions could be the quality of photolithography used in production of microfluidic devices.<var>Using given results we can now calculate the required width of the channel in order to produce liposomes of needed size as well as synthesize them in whole range of 5-30 µm. | <p>As we can see, channel width has a huge impact on the size of liposomes. Even by keeping flow rates of all phases the same, droplet radius variations depend solely on channel dimensions. We have tested channels from 10 µm to 15 µm, but other widths should also comply with given results and the only limit on minimal channel dimensions could be the quality of photolithography used in production of microfluidic devices.<var>Using given results we can now calculate the required width of the channel in order to produce liposomes of needed size as well as synthesize them in whole range of 5-30 µm. | ||
| Line 808: | Line 808: | ||
</ol> | </ol> | ||
</p> | </p> | ||
| + | |||
| + | |||
Revision as of 03:48, 18 October 2018
Modeling
Mathematical model
Mathematical models and computer simulations provide a great way to describe the function and operation of BioBrick Parts and Devices. Synthetic Biology is an engineering discipline, and part of engineering is simulation and modeling to determine the behavior of your design before you build it. Designing and simulating can be iterated many times in a computer before moving to the lab. This award is for teams who build a model of their system and use it to inform system design or simulate expected behavior in conjunction with experiments in the wetlab