(→Adapt the equation to our model, discretization) |
(→Adapt the equation to our model, discretization) |
||
| Line 163: | Line 163: | ||
<li>Splitting time and space | <li>Splitting time and space | ||
We firstly need to split each time an space variable in order to compute the variable at each point and time. | We firstly need to split each time an space variable in order to compute the variable at each point and time. | ||
| − | Here, we splitted the coordinates | + | Here, we splitted the coordinates with the same value, noted \(\Delta a\) (with a either x, y or t) for each type of coordinates. It is written as follows : |
| − | + | ||
| − | with the same value, noted \(\Delta a\) (with a either x, y or t) for each type of coordinates. It is written as follows : | + | |
| Line 186: | Line 184: | ||
<li>Discretization of the equation | <li>Discretization of the equation | ||
| − | We now need to translate the equation from a continuous to a discrete way, in order to make the computation of the solution possible. There is 3 elements to be descretized in our equation: \(\frac{\partial c}{\partial t}\), \(\frac{\partial^2 c}{\partial x^2}\) and \(\frac{\partial^2 c}{\partial y^2}\). In the first case, the partial derivative can be discretized as follows: | + | <br>We now need to translate the equation from a continuous to a discrete way, in order to make the computation of the solution possible. There is 3 elements to be descretized in our equation: \(\frac{\partial c}{\partial t}\), \(\frac{\partial^2 c}{\partial x^2}\) and \(\frac{\partial^2 c}{\partial y^2}\). In the first case, the partial derivative can be discretized as follows: |
| Line 197: | Line 195: | ||
| − | With \(c(x_i,y_j,t_n) = c^n_{i,j}\), and so \(c(x_i,y_j,t_n + \Delta t) = c^{n + \Delta t}_{i,j}\) | + | <br>With \(c(x_i,y_j,t_n) = c^n_{i,j}\), and so \(c(x_i,y_j,t_n + \Delta t) = c^{n + \Delta t}_{i,j}\) |
For the other 2 partial derivatives, they wil be discretized as follows : | For the other 2 partial derivatives, they wil be discretized as follows : | ||
| Line 210: | Line 208: | ||
| − | The equation can than be written as : | + | <br>The equation can than be written as : |
| Line 223: | Line 221: | ||
<li>Solving the equation thanks to discretized equation | <li>Solving the equation thanks to discretized equation | ||
| − | Once simplified, the approximate solution of the discretized equation can be written as follows : | + | <br>Once simplified, the approximate solution of the discretized equation can be written as follows : |
Revision as of 18:21, 17 October 2018
Modeling
We decided to model the deployment of our bed bug trap in a realistic environment, to understand how it was likely to work and what parameters might be important. This task involved a number of different modeling tasks, that posed different problems: modeling the diffusion of pheromones in the room coming both from a natural bed bug nest and the traps that we plan to deploy; modeling the movement of bed bugs influenced both by the pheromone field and their nest; and modeling the fungal epidemic that we plan to induce in the bed bug population.
Though the model is complex and includes many parameters, it has already allowed us to draw several conclusions, and as the model is improved and the parameters are refined other conclusions will follow. For instance, using realistic diffusion parameters it is clear that the pheromone field is relatively rapidly established and so the precise nature and concentration of pheromones is probably not critical. In contrast, the delay between infection and death of bed bugs is critical for ensuring the eradication of the nest. Our modeling thus helps understand critical aspects of the proposed design.
Why modeling? Descriptions of our goals
As our project was growing, we understood the importance of modeling our solution in order to better understand how it would work. Indeed, even if we had the opportunity to do laboratory experiments to test our traps, it would be very time consuming without the aid of modeling. A model run on a computer would allow us to better understand our results and refine the trap design and field trial protocol faster. The field and laboratory trails would also help us to parameterize our model and thus refine it. Modeling our project quickly became one of our top priorities.
When we began, we wanted to test various parameters:
- The effect of furniture
Our trap will most likely be used in a room with furniture (like a bedroom for example). Even if we have the equation to model the diffusion of gases (the Fick's laws of diffusion), this model doesn't take into account the effects of obstacles, which may have an impact on diffusion, and so on the efficiency of our traps.
- The effect of air flows
Since we will put our traps in an inhabited room, it may have openings to another room or even outside. These can cause drafts, which could have an impact on pheromone diffusion, and so on the efficiency of our traps.
This list is of course not complete and many other aspects will affect our traps efficiency and we hope to test them using our model.
Unfortunately, among the 2 parameters we initially wanted to investigate, only one of them has been successfully incorporated into the program, because of the complexity of the mathematical models and their solutions.
Through our program, we manage to discover new things about our solution, particularly about diffusion and the number of traps required to eliminate the bedbugs. Indeed, through various simulation, we manage to discover that the pheromone diffused through the space quicker than the bedbugs were. Those observations, back up by statistics studies of simulations, let us think that a great amount of traps are not required to eliminate the bedbugs successfully.
How did we model?
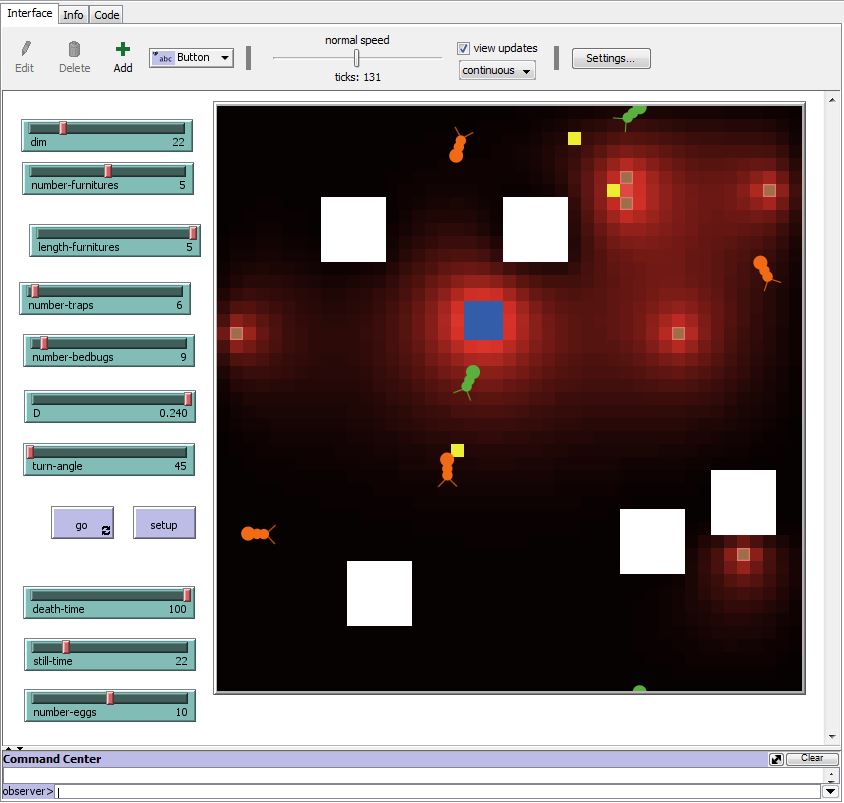
Our program has to model the diffusion of pheromones through a room containing furnitures. It needed to include the behavior of bed bugs influenced by the pheromones and to describe their deaths (caused by the fungus). This model will have to manage a lot of parameters, from the diffusion of pheromones to the bedbugs movement and the interactions between all these variables. Because of the complexity of the phenomena, building the program by describing every action occurring in our model would be too difficult. Fortunately for us, we could use the language NetLogo, which allowed us to use agent-based modeling, a type of modeling particularly efficient for complex system modeling.
Agent-based modeling allows us to define the behavior of the agents (the diffusing molecules, the bedbugs,...) by defining the interactions between those agents. With the NetLogo language, those agents are patches, representing the environment where other agents are interacting and the turtles, mobile agents who can move through the world made by patches and interact with the other agents (patches or turtles). Those agents allowed us to build our current program. Thanks to this, modeling systems with multiples agents are interacting with every other agent is simpler.
What did we Model ?
Modeling Diffusion
When we begin the development of our project, we first searched on the iGEM's database, in order to find if any teams had already worked on pheromone diffusion. After a few research among the previous iGEM's teams, we found out that the Valencia team of 2014 had also worked on pheromone diffusion and had modeled it using NetLogo. Because of the similarity between their work and ours, we inspired ourselves with the design of their modeling of diffusion when we model this aspect.
Fick's law of diffusion, mathematical model
As the 2014 Valencia team already found out, there is many ways to model diffusion. Here, we will use the Fick's law of diffusion to model it because of its simplicity and the amount of documentation about it we have access to. But there could be an impact of diffusion within a fluid in motion, the effect of air flows on diffusion, this can be modeled by the Navier-Stokes equations. Here we choose to not use it and hypothesize a room without drafts, but since it is the subject of another aspect of the program, we will develop it later.
How the equation is used in our model
The most well known form of the Fick's law of diffusion is described as it follows :
\begin{equation}
\frac{\partial c}{\partial t} = {\nabla(D,c)}
\end{equation}
It is a partial differential equation with D being the diffusion coefficient, c being the pheromone concentration and \(\nabla\) being the gradient operator.
Since we consider our diffusion coefficient as constant, the equation can be set as:
\begin{equation}
\frac{\partial c}{\partial t} = D\times\nabla^2 c = D\times\Delta c
\end{equation}
With \(\Delta\) being the Laplacian operator. This equation is called the Heat equation and is well known to model various transfer problems. In our case, this equation models the diffusion of pheromones, in the absence air flow. In a 2D environment, the equation would be :
\begin{equation}
\frac{\partial c}{\partial t} = D\times\Delta c = D\times(\frac{\partial^2 c}{\partial x^2} + \frac{\partial^2 c}{\partial y^2})
\end{equation}
Adapt the equation to our model, discretization
Even though we have our mathematical model, we still have to adapt it to our program. In order to do it, we use the finite difference method to approximate the solution of our equation. This method allows the program to compute on every position the approximate solution of our equation. By this, we are able to monitor the diffusion of the phermones at each point in time and space. Finite difference method can be achieved through various ways. Here, and even though the implicit method is stabler we choose the Euler's explicit method, since it is the simplest method for us to use.
This method allow discretization through 3 steps :
- Splitting time and space We firstly need to split each time an space variable in order to compute the variable at each point and time. Here, we splitted the coordinates with the same value, noted \(\Delta a\) (with a either x, y or t) for each type of coordinates. It is written as follows : \begin{equation} x_i = i\times\Delta x \end{equation} \begin{equation} y_j = j\times\Delta y \end{equation} \begin{equation} t_n = n\times\Delta t \end{equation}
- Discretization of the equation
We now need to translate the equation from a continuous to a discrete way, in order to make the computation of the solution possible. There is 3 elements to be descretized in our equation: \(\frac{\partial c}{\partial t}\), \(\frac{\partial^2 c}{\partial x^2}\) and \(\frac{\partial^2 c}{\partial y^2}\). In the first case, the partial derivative can be discretized as follows: \begin{equation} \frac{\partial c}{\partial t} = \frac{c^{n+\Delta t}_{i,j} - c^n_{i,j}}{\Delta t} \end{equation}
With \(c(x_i,y_j,t_n) = c^n_{i,j}\), and so \(c(x_i,y_j,t_n + \Delta t) = c^{n + \Delta t}_{i,j}\) For the other 2 partial derivatives, they wil be discretized as follows : \begin{equation} \frac{\partial^2 c}{\partial x^2} = \frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} \end{equation} \begin{equation} \frac{\partial^2 c}{\partial y^2} = \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2} \end{equation}
The equation can than be written as : \begin{equation} \frac{c^{n+\Delta t}_{i,j} - c^n_{i,j}}{\Delta t} = D\times(\frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} + \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2}) \end{equation} - Solving the equation thanks to discretized equation
Once simplified, the approximate solution of the discretized equation can be written as follows : \begin{equation} c^{n + \Delta t}_{i,j} = D\times(\frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} + \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2})\times\Delta t + c^n_{i,j} \end{equation}-
To avoid instability, we need to fulfill the condition \(\frac{D\times\Delta t}{\Delta x^2}\leqslant \frac{1}{2}\).
Modeling the impact of furnitures
Since the pheromone will diffuse in a room containing furnitures, we had to take into account that they could impact on diffusion. We will integrate it to our program thanks to the computation of the effective diffusion coefficient \(D_eff\). The computation will be realized thanks to a modified Maxwell-Garnett equation.
This equation is generally used to solve problems of transport in composite materials. Here, we will use it to compute the effective diffusion coefficient in a case where the environment is composed of square inclusions inside the general environment (here the furnitures included inside the room).
Usually the Maxwell-Garnett equation (if the diffusion is studied) is described as follow:
\begin{equation}
\frac{D_eff - D_m}{D_eff + 2\times D_m} = \phi(\frac{D_i - D_m}{D_i + 2\times D_m})
\end{equation}
With \(D_m\) beeing the diffusion coefficient of the environment, \(D_i\) beeing the diffusion coefficient inside the inclusions and \(\phi = \frac{V^d_i}{V^d_m}\) with \(V_i\) the volume of the inclusions and \(V_m\) the volume of the environment. Because of our 2D environment, we will compute area instead of volumes. They will be compute with the length of the furnitures (for the area of the inclusions) and the length of the entire world (for the area of the environment).
From this equation, and with an environment in 2D, we can set \(D_eff\) as follows:
\begin{equation} D_eff = D_m \times (1 + \frac{2 \times \phi \times (D_i - D_m)}{D_i + D_m - \phi \times (D_i - D_m)}) \end{equation}
But, here, the inclusions (the furnitures) can't be crossed by pheromones. After applying a correction to the equation in order to take account of this impenetrability, the equation describing \(D_eff\) in our case can be written as follow:
\begin{equation} D_eff = \frac{D_m}{1 + \phi} \times (1 - \frac{2 \times \phi}{1 + \phi}) \end{equation}
Modeling the Bedbugs behaviour, movements and death
Now we have modeled the diffusion of the pheromones through the room, we have now to modeled the behaviour of the bedbugs in this environment.
bedbugs entering in copntact with the trap are infected by the fungus. at this moment a timer, determined by the observer (thanks to a slider) start. note that the program create a bit of uncertainty on the duration betwin the infection and the death (+/- 10%). at the end of the timer, the bedbug die.
to speak about the nest, it contain a certain number of egg, determined by the observber (thanks to a slider). if a bedbug infected by the fungus go back to the nest, it decrease by one the number of egg in the nest. if the number of egg in the nest reach 0, the nest is destroied.