(→Cycle of runnings) |
|||
| Line 338: | Line 338: | ||
</div> | </div> | ||
<div class="column full size"> | <div class="column full size"> | ||
| + | |||
| + | |||
| + | ==Results== | ||
Revision as of 22:36, 17 October 2018
Modeling
We decided to model the deployment of our bed bug trap in a realistic environment, to understand how it was likely to work and what parameters might be important. This task involved a number of different modeling tasks, that posed different problems: modeling the diffusion of pheromones in the room coming both from a natural bed bug nest and the traps that we plan to deploy; modeling the movement of bed bugs influenced both by the pheromone field and their nest; and modeling the fungal epidemic that we plan to induce in the bed bug population.
Though the model is complex and includes many parameters, it has already allowed us to draw several conclusions, and as the model is improved and the parameters are refined other conclusions will follow. For instance, using realistic diffusion parameters it is clear that the pheromone field is relatively rapidly established and so the precise nature and concentration of pheromones is probably not critical. In contrast, the delay between infection and death of bed bugs is critical for ensuring the eradication of the nest. Our modeling thus helps understand critical aspects of the proposed design.
Contents
Why modeling? Descriptions of our goals
As our project was growing, we understood the importance to model our solution in order to better understand how it would work. Indeed, even if we had the opportunity to make laboratory experiments to test our traps, it would take to much time without the help of modelling. A model run on a computer would allow us to better understand our results and improve the trap design. The field and laboratory trials would also help us to adjust our model and thus refine it. So, modelling our project quickly became one of our top priorities.
When we began, we wanted to test various parameters:
- The effect of furniture
Our trap will most likely be used in a room with furniture (like a bedroom for example). Even if we have the equation to model the diffusion of gases (the Fick's laws of diffusion), this model doesn't involve effects of obstacles, which may have an impact on diffusion, and so on the efficiency of our traps.
- The effect of air flows
We will put our traps in an inhabited room, so it may have openings on another room even outside. These can cause drafts, which could have an impact on pheromone diffusion, and so on the efficiency of our traps.
This list is, of course, not complete and many other aspects will affect our trap efficiency and we hope to test them using our model.
Unfortunately, among 2 parameters we initially wanted to investigate, only one of them has been successfully incorporated into the program because of the complexity of the mathematical models and their solutions.
Through our program, we manage to discover new things about our solution, particularly about diffusion and the number of traps required to eliminate the bedbugs. Indeed, through various simulations, we manage to discover that the pheromone diffused through the space quicker than the bedbugs were. Those observations, back up by statistics studies of simulations, let us think that a great amount of traps are not required to eliminate successfully the bed bugs.
How did we model?
Our program has to model the diffusion of pheromones through a room containing furnitures. It needed to include the behavior of bed bugs influenced by the pheromones and to describe their deaths (caused by the fungus). This model will have to manage a lot of parameters, from the diffusion of pheromones to the bedbugs movement and the interactions between all these variables. Because of the complexity of the phenomena, building the program by describing every action occurring in our model would be too difficult. Fortunately for us, we could use the language NetLogo, which allowed us to use agent-based modeling, a type of modeling particularly efficient for complex system modeling.
Agent-based modeling allows us to define the behavior of the agents (the diffusing molecules, the bedbugs,...) by defining the interactions between those agents. With the NetLogo language, those agents are patches, representing the environment where other agents are interacting and the turtles, mobile agents who can move through the world made by patches and interact with the other agents (patches or turtles). Those agents allowed us to build our current program. Thanks to this, modeling systems with multiples agents are interacting with every other agent is simpler.
What did we Model ?
Modeling Diffusion
When we begin the development of our project, we first searched on the iGEM's database, in order to find if any teams had already worked on pheromone diffusion. After a few research among the previous iGEM's teams, we found out that the Valencia team of 2014 had also worked on pheromone diffusion and had modeled it using NetLogo. Because of the similarity between their work and ours, we inspired ourselves with the design of their modeling of diffusion when we model this aspect.
Fick's law of diffusion, mathematical model
As the 2014 Valencia team already found out, there is many ways to model diffusion. Here, we will use the Fick's law of diffusion to model it because of its simplicity and the amount of documentation about it we have access to. But there could be an impact of diffusion within a fluid in motion, the effect of air flows on diffusion, this can be modeled by the Navier-Stokes equations. Here we choose to not use it and hypothesize a room without drafts, but since it is the subject of another aspect of the program, we will develop it later.
How the equation is used in our model
The most well known form of the Fick's law of diffusion is described as it follows :
\begin{equation}
\frac{\partial c}{\partial t} = {\nabla(D,c)}
\end{equation}
It is a partial differential equation with D being the diffusion coefficient, c being the pheromone concentration and \(\nabla\) being the gradient operator.
Since we consider our diffusion coefficient as constant, the equation can be set as:
\begin{equation}
\frac{\partial c}{\partial t} = D\times\nabla^2 c = D\times\Delta c
\end{equation}
With \(\Delta\) being the Laplacian operator.
This equation is called the Heat equation and is well known to model various transfer problems.
In our case, this equation models the diffusion of pheromones, in the absence air flow.
In a 2D environment, the equation would be :
\begin{equation}
\frac{\partial c}{\partial t} = D\times\Delta c = D\times(\frac{\partial^2 c}{\partial x^2} + \frac{\partial^2 c}{\partial y^2})
\end{equation}
Adapt the equation to our model, discretization
Even though we have our mathematical model, we still have to adapt it to our program. In order to do it, we use the finite difference method to approximate the solution of our equation. This method allows the program to compute on every position the approximate solution of our equation. By this, we are able to monitor the diffusion of the phermones at each point in time and space. Finite difference method can be achieved through various ways. Here, and even though the implicit method is stabler we choose the Euler's explicit method, since it is the simplest method for us to use.
This method allow discretization through 3 steps :
- Splitting time and space
We firstly need to split each time an space variable in order to compute the variable at each point and time.
Here, we splitted the coordinates with the same value, noted \(\Delta a\) (with a either x, y or t) for each type of coordinates. It is written as follows :
\begin{equation} x_i = i\times\Delta x \end{equation} \begin{equation} y_j = j\times\Delta y \end{equation} \begin{equation} t_n = n\times\Delta t \end{equation}
- Discretization of the equation
We now need to translate the equation from a continuous to a discrete way, in order to make the computation of the solution possible. There is 3 elements to be descretized in our equation: \(\frac{\partial c}{\partial t}\), \(\frac{\partial^2 c}{\partial x^2}\) and \(\frac{\partial^2 c}{\partial y^2}\). In the first case, the partial derivative can be discretized as follows:
\begin{equation} \frac{\partial c}{\partial t} = \frac{c^{n+\Delta t}_{i,j} - c^n_{i,j}}{\Delta t} \end{equation}
With \(c(x_i,y_j,t_n) = c^n_{i,j}\), and so \(c(x_i,y_j,t_n + \Delta t) = c^{n + \Delta t}_{i,j}\)
For the other 2 partial derivatives, they wil be discretized as follows :
\begin{equation} \frac{\partial^2 c}{\partial x^2} = \frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} \end{equation} \begin{equation} \frac{\partial^2 c}{\partial y^2} = \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2} \end{equation}
The equation can than be written as :
\begin{equation} \frac{c^{n+\Delta t}_{i,j} - c^n_{i,j}}{\Delta t} = D\times(\frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} + \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2}) \end{equation}
- Solving the equation thanks to discretized equation
Once simplified, the approximate solution of the discretized equation can be written as follows :
\begin{equation} c^{n + \Delta t}_{i,j} = D\times(\frac{c^n_{i + \Delta x,j} + c^n_{ i - \Delta x,j} - 2\times c^n_{i,j}}{\Delta x^2} + \frac{c^n_{i,j + \Delta y} + c^n_{i,j - \Delta y} - 2\times c^n_{i,j}}{\Delta y^2})\times\Delta t + c^n_{i,j} \end{equation}
To avoid instability, we need to fulfill the condition \(\frac{D\times\Delta t}{\Delta x^2}\leqslant \frac{1}{2}\).
Modeling the impact of furnitures
Since the pheromone will diffuse in a room containing furnitures, we had to take into account that they could impact on diffusion. We will integrate it to our program thanks to the computation of the effective diffusion coefficient \(D_eff\). The computation will be realized thanks to a modified Maxwell-Garnett equation.
This equation is generally used to solve problems of transport in composite materials. Here, we will use it to compute the effective diffusion coefficient in a case where the environment is composed of square inclusions inside the general environment (here the furnitures included inside the room).
Usually the Maxwell-Garnett equation (if the diffusion is studied) is described as follow:
\begin{equation} \frac{D_eff - D_m}{D_eff + 2\times D_m} = \phi(\frac{D_i - D_m}{D_i + 2\times D_m}) \end{equation}
With \(D_m\) beeing the diffusion coefficient of the environment, \(D_i\) beeing the diffusion coefficient inside the inclusions and \(\phi = \frac{V^d_i}{V^d_m}\) with \(V_i\) the volume of the inclusions and \(V_m\) the volume of the environment.
Because of our 2D environment, we will compute area instead of volumes. They will be compute with the length of the furnitures (for the area of the inclusions) and the length of the entire world (for the area of the environment).
From this equation, and with an environment in 2D, we can set \(D_eff\) as follows:
\begin{equation} D_eff = D_m \times (1 + \frac{2 \times \phi \times (D_i - D_m)}{D_i + D_m - \phi \times (D_i - D_m)}) \end{equation}
But, here, the inclusions (the furnitures) can't be crossed by pheromones. After applying a correction to the equation in order to take account of this impenetrability, the equation describing \(D_eff\) in our case can be written as follow:
\begin{equation} D_eff = \frac{D_m}{1 + \phi} \times (1 - \frac{2 \times \phi}{1 + \phi}) \end{equation}
Modeling the Bedbugs behaviour, movements and death
Movements of the bedbugs
Now we have modeled the diffusion of the pheromones through the room, we have now to modeled the behaviour of the bedbugs in this environment. We firstly visualized the movement of our bedbugs as random when they are not in contact with any pheromones. Then, as soon as they are in contact with pheromones, the randomness of their behaviour is limited by the attraction of the high quantity of pheromones. Since pheromones are used to attract bedbugs to the traps, only 2 structures will emit pheromones, the traps, in order to model our solution, and the nest, modeling the place where the bedbug go back.
Concretely, when the bedbug is not in contact with a patch containing pheromones, we designed the bedbug to walk randomly across the environment, thanks to a group of ifelses instructions and an increasing randomness code. When the bedbug is near a patch containing pheromones, the bedbug is oriented facing the patch with the higher quantity of pheromones. Then, the bedbug moves forward to the patch the bedbug is facing, but with a bit of randomness again. It is important to note that the bedbugs has a minimum and a maximum pheromone detection threshold. Those thresholds limit the attractive effect of the pheromones, making the model more realistic.
We also implemented some particular movements behaviour in the case a bedbug had to interact with a specific patch, such as furnitures, traps or the nest. When the bedbug is facing a furniture, it will be oriented at the opposite from the furniture before moving forward randomly. In the case of the nest, the bedbug is stop by the histamin contained in the nest. A few moments later, the bedbug is set facing another direction and move forward.
Death mechanisms of the bedbugs and their nest
Another particular behaviour is triggered by the infection of the bedbugs by the fungus and the deaths of the infected bedbugs. When a Bedbug is in front of a trap, the program color the bedbug in orange and set off a timer. It represent the life time left to the bedbug from its infection and is unique for each bedbug. When that timer is finished, the bedbug die and color the patch below in yellow. That patch, the corpse of the bedbug, can also infect other bedbug and contribute to the propagation of the infection.
Another particular situation is when an infected bedbug dies next to the nest. In that case, the fungus will spread to the bedbugs inside the nest, adults and younger individuals (like eggs). In order to model this, we give the nest a value, representing the number of time the nest can withstand the death of an infected bedbug next to it. Each time a bedbug die this way, this counter is decreased by one, and when it gets to 0, the nest is destroyed, representing the infection of every individuals inside the nest.
Simulation routine
The Netlogo environment can be downloaded on it website, at the Nothwestern University. The source file of our program is available here.
Initialization
When the program is set up, 4 types of agents are created:
- bedbugs: each of them will have 2 major features. The lifetime available after the infection, the amount of time the bedbug will be immobilized in front of the nest.
- traps: they will diffuse pheromones and start the infection of bedbug.
- furnitures: impenetrable obstacles for any other agents
- nest: location where the bedbugs go back after exploration
During this step, the program also compute the effective diffusion coefficient, and prepare the environment for diffusion.
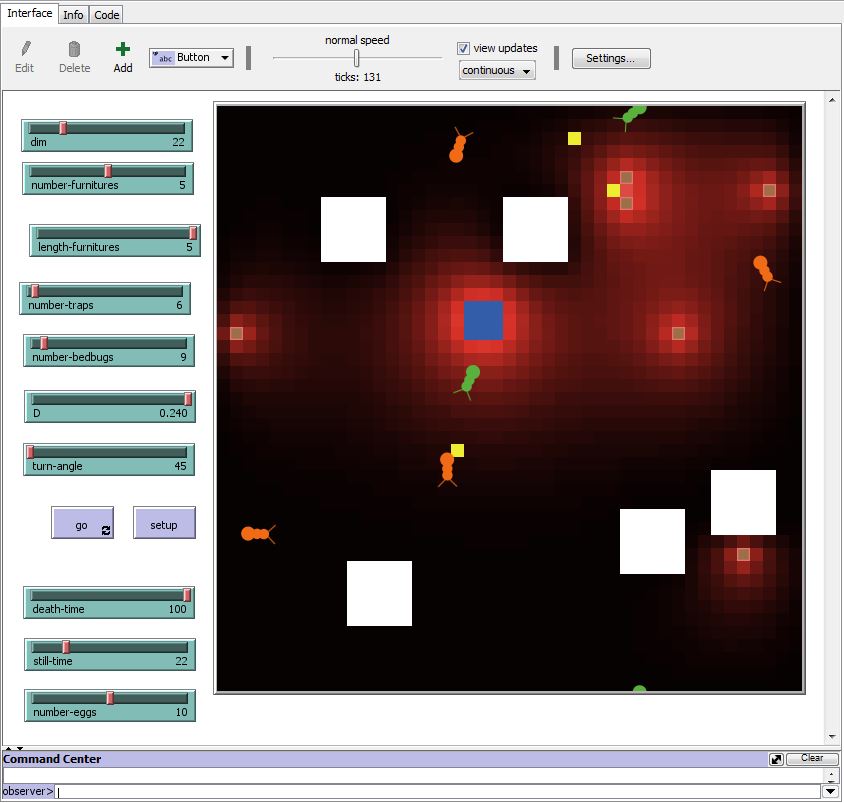
Cycle of runnings
During a run, the program compute the quantity of pheromones in every patch and make a color scale with it. The more pheromones are in the patch, the more the color of the patch is red. Thanks to this computation, the bedbugs can guide themselves towards the higher quantity of pheromone. After this calculation step, the program manage the specific interaction between bedbugs and the nest. Following this step, the bedbugs moves through the environment. Finally, the infection and deaths mechanisms are setted up.