YKristiansen (Talk | contribs) |
|||
| Line 14: | Line 14: | ||
===Implementation=== | ===Implementation=== | ||
===Results=== | ===Results=== | ||
| + | For the calculations of the desired values, two pairs of data points are considered. | ||
| + | The used values are from two reaction mixtures and the data of the f‑values comes from NMR analysis of the molar ratio of the two monomers in the polymer. | ||
| + | <br> | ||
| + | The used data points are: | ||
| + | <br> | ||
| + | {|class="wikitable" | ||
| + | |- | ||
| + | ! | ||
| + | !reaction 1 | ||
| + | !reaction 2 | ||
| + | |- | ||
| + | |F | ||
| + | |75/25 | ||
| + | |2/3 / 1/3 | ||
| + | |- | ||
| + | |f | ||
| + | |59.13/40.87 | ||
| + | |38.76/61.24 | ||
| + | |} | ||
| + | <br> | ||
| + | From the experimental data, the values for H can be calculated. | ||
| + | <br> | ||
| + | [// image link H-value calculation] | ||
| + | <br> | ||
| + | When different H‑ values are known, the helping variable α can be calculated and incorporated into the Kelen‑Tuedos‑equation. | ||
| + | In combination with the experimental data points, a linear equation system is made to calculate r<sub>1</sub> and r<sub>2</sub> as follows: | ||
| + | <br> | ||
| + | [// image K-T linear equation system] | ||
| + | <br> | ||
| + | Now that the two needed copolymerization parameters are known, the final composition of monomers in a polymer can be calculated with the equation: | ||
| + | <br> | ||
| + | [https://static.igem.org/mediawiki/2018/8/81/T--TU_Darmstadt--kelen-tudosnachf.png] | ||
| + | <br> | ||
| + | In the following table are different theoretical monomer compositions in correlation to the used starting monomer composition listed as calculated. | ||
| + | <br> | ||
| + | {|class="wikitable" | ||
| + | |- | ||
| + | ! F | ||
| + | ! f | ||
| + | |- | ||
| + | |1.5 | ||
| + | |0.2735 | ||
| + | |- | ||
| + | |2 | ||
| + | |0.668 | ||
| + | |- | ||
| + | |2.5 | ||
| + | |1.0625 | ||
| + | |- | ||
| + | |3 | ||
| + | |1.8515 | ||
| + | |- | ||
| + | |3.5 | ||
| + | |1.8515 | ||
| + | |- | ||
| + | |4 | ||
| + | |2.246 | ||
| + | |- | ||
| + | |4.5 | ||
| + | |2.6405 | ||
| + | |- | ||
| + | |5 | ||
| + | |3.4295 | ||
| + | |} | ||
| + | <br> | ||
| + | The calculated data is an approximation if the yield of polymer is smaller than 50% and if F is bigger than 1.25. | ||
| + | <br> | ||
| + | <br> | ||
===Conclusion=== | ===Conclusion=== | ||
| + | The calculated r‑values with r<sub>1</sub>=0.84 and r<sub>2</sub>=1.04 show that glycolide is slightly better incorporated into the polymer than lactide. | ||
| + | This yields a stochastic alternating copolymer with more glycolide in the final polymer than lactide, at least for the observed conversion rates of about 20& polymer production. | ||
| + | When the polymer yield increases further and goes against 100%, the observed polymer composition will be the starting composition. | ||
| + | To improve these calculations, more data points can be used to yield a more exact value for α and with a better approximation for α the copolymerization parameters will be better to describe our process. | ||
| + | For that additional reaction mixtures and respective ratios need to be determined by NMR spectroscopy, but nevertheless we achieved to calculate the obtained monomer ratio of a co-polymer consisting of lactide and glycolide with a given starting ratio for the reaction. | ||
| + | |||
| + | |||
| + | |||
| + | |||
===Outlook=== | ===Outlook=== | ||
Revision as of 15:29, 15 October 2018
Contents
Modeling
Abstract
For this year's project we wanted to predict the composition of our polymer. This is very important for our project, because the reaction of our different monomers during the polymerization influence the properties like the crystallinity of the polymer and through that also our application approach. For medical applications it is necessary to have a defined composition and thereby specific properties of the used polymer for example to prevent inflammatory reactions.
We came across that idea through a conversation with Evonik Industries which is a company focused on the production of specialty chemicals. Because of Evonik’s remark concerning the probability of binding our different monomers we decided to develop a kinetic model. Evonik explained that glycolic acid will incorporate better than lactic acid in our polymer but they were not allowed to tell us in which amount. This led to different properties of the polymer, because of the possible formation of blocks of glycolic acid during the polymerization. Therefore, we focused on the kinetic model to obtain its composition and predict properties of our synthesized polymer, concerning different ratio of monomers.
Introduction
Implementation
Results
For the calculations of the desired values, two pairs of data points are considered.
The used values are from two reaction mixtures and the data of the f‑values comes from NMR analysis of the molar ratio of the two monomers in the polymer.
The used data points are:
| reaction 1 | reaction 2 | |
|---|---|---|
| F | 75/25 | 2/3 / 1/3 |
| f | 59.13/40.87 | 38.76/61.24 |
From the experimental data, the values for H can be calculated.
[// image link H-value calculation]
When different H‑ values are known, the helping variable α can be calculated and incorporated into the Kelen‑Tuedos‑equation.
In combination with the experimental data points, a linear equation system is made to calculate r1 and r2 as follows:
[// image K-T linear equation system]
Now that the two needed copolymerization parameters are known, the final composition of monomers in a polymer can be calculated with the equation:
[1]
In the following table are different theoretical monomer compositions in correlation to the used starting monomer composition listed as calculated.
| F | f |
|---|---|
| 1.5 | 0.2735 |
| 2 | 0.668 |
| 2.5 | 1.0625 |
| 3 | 1.8515 |
| 3.5 | 1.8515 |
| 4 | 2.246 |
| 4.5 | 2.6405 |
| 5 | 3.4295 |
The calculated data is an approximation if the yield of polymer is smaller than 50% and if F is bigger than 1.25.
Conclusion
The calculated r‑values with r1=0.84 and r2=1.04 show that glycolide is slightly better incorporated into the polymer than lactide. This yields a stochastic alternating copolymer with more glycolide in the final polymer than lactide, at least for the observed conversion rates of about 20& polymer production. When the polymer yield increases further and goes against 100%, the observed polymer composition will be the starting composition. To improve these calculations, more data points can be used to yield a more exact value for α and with a better approximation for α the copolymerization parameters will be better to describe our process. For that additional reaction mixtures and respective ratios need to be determined by NMR spectroscopy, but nevertheless we achieved to calculate the obtained monomer ratio of a co-polymer consisting of lactide and glycolide with a given starting ratio for the reaction.
Outlook
For a further and more detailed understanding of our polymerization process there is the possibility to create a molecular dynamics (MD) simulation.
In general, molecular dynamics simulations are calculated interactions between atoms with defined forces and properties. This method is normally used to model protein folding processes and interactions, but can also be modified to simulate polymerization steps, such as the anionic ring-opening polymerization we used in our project.
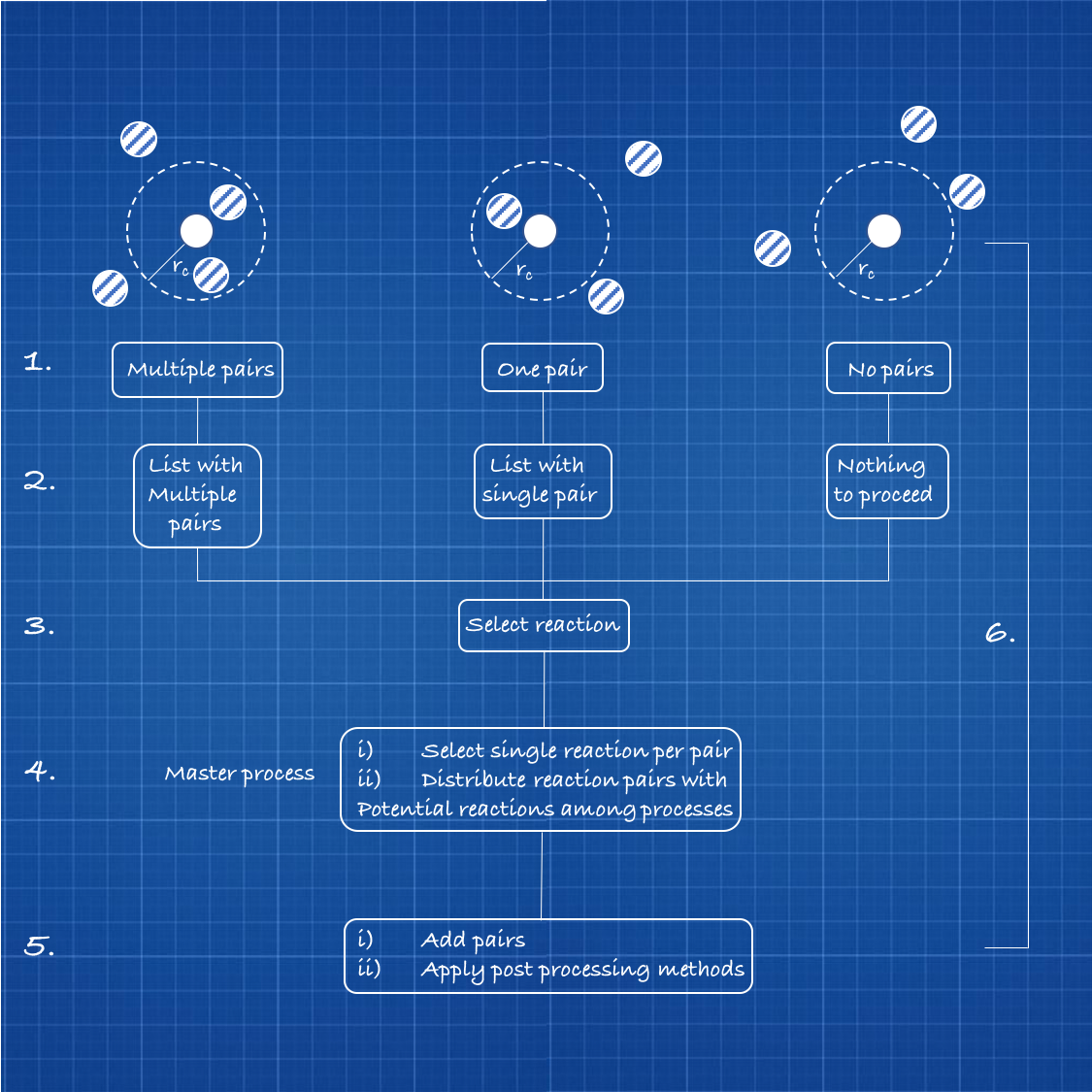
In theory, it is possible to simplify the reacting atoms as functional groups in a so-called coarse-grained model. Each functional group is then displayed as one particle with a defined reaction radius. For every particle a specific potential is defined that describes its binding affinity towards other particles.
As displayed in figure 1, the first step of the simulation is setting up the particles in a reaction space. For this, a Lennard-Jones potential is used to give all particles the ability to recognize other particles in a specific cut-off radius [1.]
Then, the algorithm generates a list of all the potential binding partners [2.].
The next step is to select all the possible bonds [3].
After this, one bonding interaction is randomly chosen and the bonding potential is determined [4]. The bond between the particles is finally fulfilled and post process methods are applied. These include a reset of the bond list, a redefining of binding affinity potentials of the new build particle groups, and a characterization of ghost particles, that are already bound to as many particles, as they possibly can.
The ghost particles are then not able to react anymore [5.].
To simulate further polymer chain growth these five steps are looped as many times as there are still particles, that are capable to react [6.].
Figure 1: Displayed of a theoretical six-step procedure of a molecular dynamic simulation for particle reactions.
However, since there was not enough time to realize this part of the project, we were not able to create the full simulation. But if the MD simulation would have been successful, it would have made a major impact on the optimization of our experimental polymer synthesis. With its results it would have been possible to predict the average chain length and monomer ratio. This would then make it possible to synthesize a predictable polymer.